题目内容
(16分)已知数列 ,
,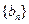 满足
满足 ,其中
,其中 .
.
(1)若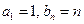 ,求数列
,求数列 的通项公式;
的通项公式;
(2)若 ,且
,且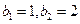 .记
.记 ,
,
求证:数列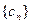 为等差数列;
为等差数列;
 ,
,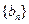 满足
满足 ,其中
,其中 .
.(1)若
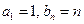 ,求数列
,求数列 的通项公式;
的通项公式;(2)若
 ,且
,且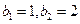 .记
.记 ,
,求证:数列
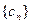 为等差数列;
为等差数列;解 (1
(1 )当
)当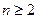 时,有
时,有
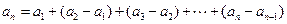
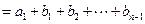 …………4分
…………4分
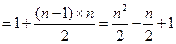 . ………………6分
. ………………6分
又因为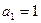 也满足上式,所以数列
也满足上式,所以数列 的通项为
的通项为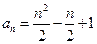 .………………7分
.………………7分
(2)由题设知: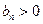 ,对任意的
,对任意的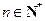 有
有
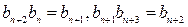 得
得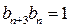 ,
,
于是又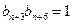 , 故
, 故 ……………………………………………9分
……………………………………………9分
∴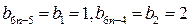 ,
,
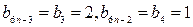 ,
,
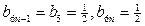
∴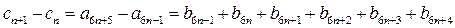
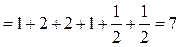
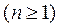 ,
,
所以数列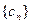 为等差数列. …………………………16分
为等差数列. …………………………16分
 (1
(1 )当
)当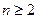 时,有
时,有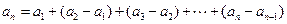
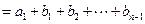 …………4分
…………4分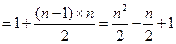 . ………………6分
. ………………6分又因为
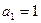 也满足上式,所以数列
也满足上式,所以数列 的通项为
的通项为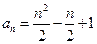 .………………7分
.………………7分(2)由题设知:
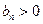 ,对任意的
,对任意的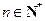 有
有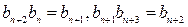 得
得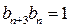 ,
,于是又
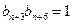 , 故
, 故 ……………………………………………9分
……………………………………………9分∴
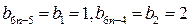 ,
,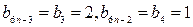 ,
,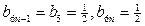
∴
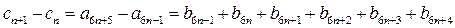
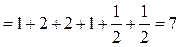
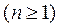 ,
,所以数列
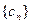 为等差数列. …………………………16分
为等差数列. …………………………16分略

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
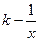 (x>0),且已知投入广告费1万元时,年销量为2万件产品.预计此种产品年销售收入M(万元)等于年成本(万元)(年成本中不含广告费用)的150%与年广告费用(万元)的50%的和.
(x>0),且已知投入广告费1万元时,年销量为2万件产品.预计此种产品年销售收入M(万元)等于年成本(万元)(年成本中不含广告费用)的150%与年广告费用(万元)的50%的和.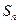 为数列
为数列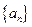 的前
的前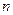 项和,且
项和,且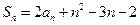 ,
,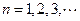 ,
,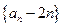 为等比数列;
为等比数列;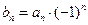 ,求数列
,求数列 的前
的前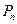 ;
;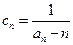 ,数列
,数列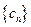 的前
的前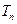 ,求证:
,求证: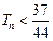 .
.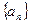 、
、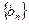 都是等
都是等 差数列,且
差数列,且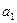 =5,
=5,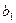 =15,
=15,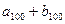 =100,则数列
=100,则数列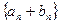 的前
的前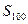 等于: ( )
等于: ( ) 、 6000 D、60000
、 6000 D、60000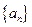 是等差数列,若
是等差数列,若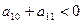 ,且
,且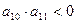 ,它的前
,它的前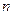 项和
项和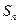 有最大值,那么当
有最大值,那么当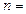 ( )
( )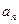 }的前n项和为
}的前n项和为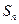 ,若
,若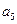 =
= 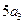 ,则
,则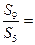
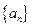 中,
中,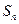 是其前
是其前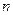 项的和,且
项的和,且 ,
, ,则数列
,则数列 的前
的前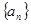 的公差大于0,且
的公差大于0,且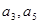 是方程
是方程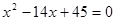 的两根,数列
的两根,数列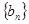 的前n项的和为
的前n项的和为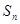 ,且
,且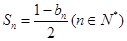 .
.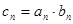 求数列
求数列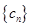 的前
的前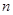 项和
项和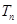 .
.