题目内容
【题目】如图，某公园摩天轮的半径为
，圆心距地面的高度为
，摩天轮做匀速转动，每
转一圈，摩天轮上的点
的起始位置在最低点处.
（1）已知在时刻
时距离地面的高度
，（其中
），求
时距离地面的高度；
（2）当离地面
以上时，可以看到公园的全貌，求转一圈中有多少时间可以看到公园的全貌？
【答案】(1)70;(2)转一圈中有
钟时间可以看到公园全貌.
【解析】分析：（1）由实际问题求出三角函数中的参数
，
，及周期
，利用三角函数的周期公式求出
，通过初始位置求出
，求出
，将
用2017代替求出2017min时点P距离地面的高度；
（2）由（1）知
，
依题意，
，求出的范围，即可求得转一圈中有钟时间可以看到公园全貌.
详解：
（1）依题意，
，则
，
且
，
故
，
∴
∴
（2）由（1）知
，
依题意，，
∴
∵
，
∴转一圈中有钟时间可以看到公园全貌.
练习册系列答案
相关题目
【题目】某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。
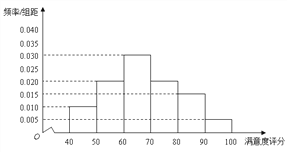
A地区用户满意度评分的频率分布直方图
B地区用户满意度评分的频数分布表
（Ⅰ）在答题卡上作出B地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）；
（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个等级：
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计哪个地区的满意度等级为不满意的概率大？说明理由
