题目内容
(2012•湖北)已知向量
=(1,0),
=(1,1),则
(Ⅰ)与2
+
同向的单位向量的坐标表示为
(Ⅱ)向量
-3
与向量
夹角的余弦值为
| a |
| b |
(Ⅰ)与2
| a |
| b |
(
,
)
3
| ||
| 10 |
| ||
| 10 |
(
,
)
;3
| ||
| 10 |
| ||
| 10 |
(Ⅱ)向量
| b |
| a |
| a |
-
2
| ||
| 5 |
-
.2
| ||
| 5 |
分析:(I)由已知可求2
+
,进而可求|2
+
|,而与2
+
同向的单位向量
,再利用坐标表示即可
(II)设
-3
与向量
夹角θ,由已知可求(
-3
)•
,|
-3
,,|
|,代入向量的夹角公式cosθ=
可求
| a |
| b |
| a |
| b |
| a |
| b |
2
| ||||
|
(II)设
| b |
| a |
| a |
| b |
| a |
| a |
| b |
| a |
| a |
(
| ||||||
|
|
解答:解:(I)∵
=(1,0),
=(1,1)
∴2
+
=(2,0)+(1,1)=(3,1),|2
+
|=
∴与2
+
同向的单位向量的坐标表示
=(
,
)
(II)设
-3
与向量
夹角θ
∵
=(1,0),
=(1,1),
∴
-3
=(1,1)-(3,0)=(-2,1),
∴(
-3
)•
=-2,|
-3
|=
=
,|
|=1
则cosθ=
=
=-
故答案为:(
,
);-
| a |
| b |
∴2
| a |
| b |
| a |
| b |
| 10 |
∴与2
| a |
| b |
2
| ||||
|
3
| ||
| 10 |
| ||
| 10 |
(II)设
| b |
| a |
| a |
∵
| a |
| b |
∴
| b |
| a |
∴(
| b |
| a |
| a |
| b |
| a |
| (-2)2+12 |
| 5 |
| a |
则cosθ=
(
| ||||||
|
|
| -2 | ||
|
2
| ||
| 5 |
故答案为:(
3
| ||
| 10 |
| ||
| 10 |
2
| ||
| 5 |
点评:本题主要考查了向量运算的坐标表示,向量的数量积的坐标表示、夹角公式的应用,注意结论:与向量
共线且同向的单位向量
的应用
| a |
| ||
|
|

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 (2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为( )
(2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为( ) (2012•湖北)已知二次函数y=f(x)的图象如图所示,则它与X轴所围图形的面积为 ( )
(2012•湖北)已知二次函数y=f(x)的图象如图所示,则它与X轴所围图形的面积为 ( )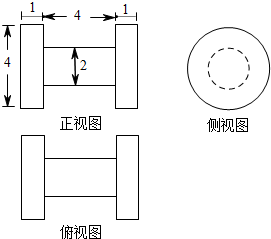 (2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为
(2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为