题目内容
 (2012•湖北)已知二次函数y=f(x)的图象如图所示,则它与X轴所围图形的面积为 ( )
(2012•湖北)已知二次函数y=f(x)的图象如图所示,则它与X轴所围图形的面积为 ( )分析:先根据函数的图象求出函数的解析式,然后利用定积分表示所求面积,最后根据定积分运算法则求出所求.
解答:解:根据函数的图象可知二次函数y=f(x)图象过点(-1,0),(1,0),(0,1)
从而可知二次函数y=f(x)=-x2+1
∴它与X轴所围图形的面积为
(-x2+1) dx=(-
+x)
=(-
+1)-(
-1)=
故选B.
从而可知二次函数y=f(x)=-x2+1
∴它与X轴所围图形的面积为
| ∫ | 1 -1 |
| x3 |
| 3 |
| | | 1 -1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
故选B.
点评:本题主要考查了定积分在求面积中的应用,解题的关键是求出被积函数,属于基础题.

练习册系列答案
相关题目
 (2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为( )
(2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为( )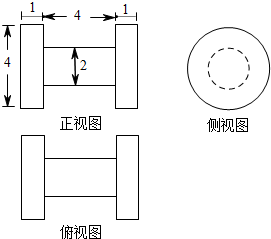 (2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为
(2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为