题目内容
(2012•湖北)已知等差数列{an}前三项的和为-3,前三项的积为8.
(1)求等差数列{an}的通项公式;
(2)若a2,a3,a1成等比数列,求数列{|an|}的前n项和.
(1)求等差数列{an}的通项公式;
(2)若a2,a3,a1成等比数列,求数列{|an|}的前n项和.
分析:(I)设等差数列的公差为d,由题意可得,
,解方程可求a1,d,进而可求通项
(II)由(I)的通项可求满足条件a2,a3,a1成等比的通项为an=3n-7,则|an|=|3n-7|=
,根据等差数列的求和公式可求
|
(II)由(I)的通项可求满足条件a2,a3,a1成等比的通项为an=3n-7,则|an|=|3n-7|=
|
解答:解:(I)设等差数列的公差为d,则a2=a1+d,a3=a1+2d
由题意可得,
解得
或
由等差数列的通项公式可得,an=2-3(n-1)=-3n+5或an=-4+3(n-1)=3n-7
(II)当an=-3n+5时,a2,a3,a1分别为-1,-4,2不成等比
当an=3n-7时,a2,a3,a1分别为-1,2,-4成等比数列,满足条件
故|an|=|3n-7|=
设数列{|an|}的前n项和为Sn
当n=1时,S1=4,当n=2时,S2=5
当n≥3时,Sn=|a1|+|a2|+…+|an|=5+(3×3-7)+(3×4-7)+…+(3n-7)
=5+
=
,当n=2时,满足此式
综上可得Sn=
由题意可得,
|
解得
|
|
由等差数列的通项公式可得,an=2-3(n-1)=-3n+5或an=-4+3(n-1)=3n-7
(II)当an=-3n+5时,a2,a3,a1分别为-1,-4,2不成等比
当an=3n-7时,a2,a3,a1分别为-1,2,-4成等比数列,满足条件
故|an|=|3n-7|=
|
设数列{|an|}的前n项和为Sn
当n=1时,S1=4,当n=2时,S2=5
当n≥3时,Sn=|a1|+|a2|+…+|an|=5+(3×3-7)+(3×4-7)+…+(3n-7)
=5+
| (n-2)[2+(3n-7)] |
| 2 |
| 3n2-11n+20 |
| 2 |
综上可得Sn=
|
点评:本题主要考查了利用等差数列的基本量表示等差数列的通项,等差数列与等比数列的通项公式的综合应用及等差数列的求和公式的应用,要注意分类讨论思想的应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为( )
(2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为( ) (2012•湖北)已知二次函数y=f(x)的图象如图所示,则它与X轴所围图形的面积为 ( )
(2012•湖北)已知二次函数y=f(x)的图象如图所示,则它与X轴所围图形的面积为 ( )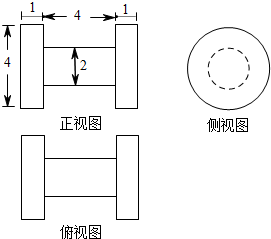 (2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为
(2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为