题目内容
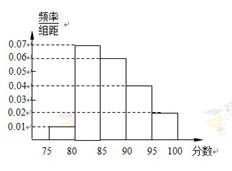
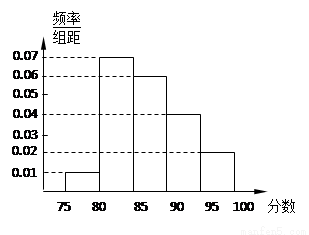
在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为 五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为
五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为 的考生有
的考生有 人.
人.

(1)求该考场考生中“阅读与表达”科目中成绩为 的人数;
的人数;
(2)若等级 分别对应
分别对应 分,
分, 分,
分, 分,
分, 分,
分, 分,求该考场考生“数学与逻辑”科目的平均分;
分,求该考场考生“数学与逻辑”科目的平均分;
(3)已知参加本考场测试的考生中,恰有两人的两科成绩均为 . 在至少一科成绩为
. 在至少一科成绩为 的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为
的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为 的概率.
的概率.
(1)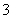 ;(2)
;(2)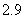 ;(3)
;(3)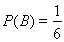 .
.
【解析】
试题分析:(1)注意根据“数学与逻辑”科目中成绩等级为B的考生有10人,计算出该考场人数.进一步计算“阅读与表达”科目中成绩为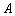 的频率乘以考场人数.
的频率乘以考场人数.
(2)利用“平均数”计算公式即得.
(3)确定两科考试中,共有6人次得分等级为A,又恰有两人的两科成绩等级均为A,
推断出有四人设为甲,乙,丙,丁,其中甲,乙是两科成绩都是A的同学,则在至少一科成绩等级为A的考生中,随机抽取两人进行访谈,写出基本事件空间:
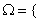 {甲,乙},{甲,丙},{甲,丁},{乙,丙},{乙,丁},{丙,丁}
{甲,乙},{甲,丙},{甲,丁},{乙,丙},{乙,丁},{丙,丁}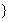 ,有6个基本事件
,有6个基本事件
两科成绩等级均为A的事件只有{甲,乙},故所求概率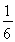 .
.
试题解析:(1)因为“数学与逻辑”科目中成绩等级为B的考生有10人,
所以该考场有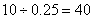 人 2分
人 2分
所以该考场考生中“阅读与表达”科目中成绩等级为A的人数为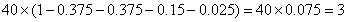 4分
4分
(2)该考场考生“数学与逻辑”科目的平均分为
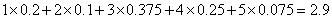 7分
7分
(3)因为两科考试中,共有6人得分等级为A,又恰有两人的两科成绩等级均为A,
所以还有2人只有一个科目得分为A,
设这四人为甲,乙,丙,丁,其中甲,乙是两科成绩都是A的同学,则在至少一科成绩等级为A的考生中,随机抽取两人进行访谈,基本事件空间为
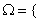 {甲,乙},{甲,丙},{甲,丁},{乙,丙},{乙,丁},{丙,丁}
{甲,乙},{甲,丙},{甲,丁},{乙,丙},{乙,丁},{丙,丁} ,有6个基本事件
,有6个基本事件
设“随机抽取两人进行访谈,这两人的两科成绩等级均为A”为事件B,所以事件B中包含的基本事件有1个,则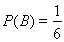 . 12分
. 12分
考点:频率分布直方图,平均数,古典概型概率的计算.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案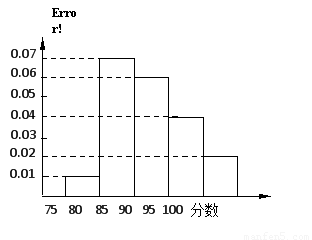
 名学生被考官L面试,求
名学生被考官L面试,求 的分布列和数学期望.
的分布列和数学期望. 名学生被考官L面试,求
名学生被考官L面试,求