题目内容
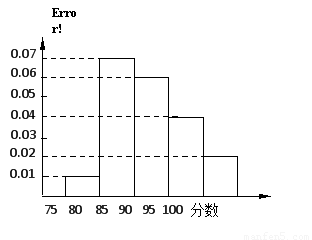
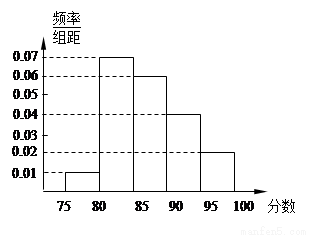
某高校在2012年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
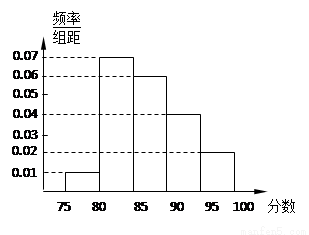
(1)分别求第3,4,5组的频率;
(2) 若该校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试。
(ⅰ) 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙恰有一人进入第二轮面试的概率;
(ⅱ) 学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官L的面试,设第4组中有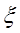 名学生被考官L面试,求
名学生被考官L面试,求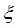 的分布列和数学期望.
的分布列和数学期望.
【答案】
解:(1) 0.3; 0.2;0.1.
(2)(ⅰ) P(A)= 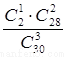
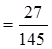
(ⅱ) 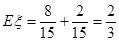
|
|
0 |
1 |
2 |
|
P |
|
|
|
【解析】本试题主要是考查了古典概型概率的计算以及分布列的求解和数学期望值的运算。
(1)利用直方图中的面积代表频率,分别求第3,4,5组的频率;
(2) 若该校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试。
已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙恰有一人进入第二轮面试的概率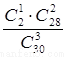 ;
;
同时学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官L的面试,设第4组中有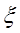 名学生被考官L面试,求
名学生被考官L面试,求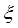 的可能取值以及各个取值的概率值,得到分布列和期望值
的可能取值以及各个取值的概率值,得到分布列和期望值

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
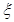
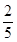
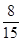
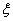
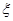 名学生被考官L面试,求
名学生被考官L面试,求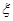 名学生被考官L面试,求
名学生被考官L面试,求