题目内容
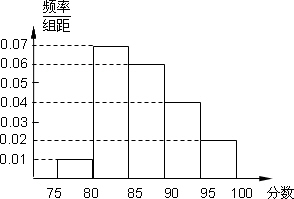
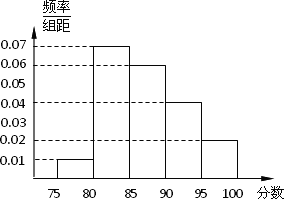
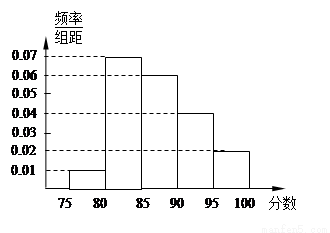
某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
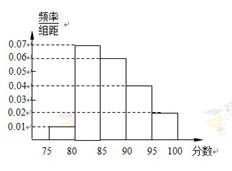
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试.
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
② 学校决定在这6名学生中随机抽取2名学生接受考官的面试,设第4组中有X名学生被考官面试,求X的分布列和数学期望.
【答案】
(1)0.3,0.2,0.1;(2)①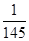 ,②分布列详见解析,
,②分布列详见解析,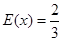 .
.
【解析】
试题分析:本题主要考查频率分布直方图的读图能力和计算能力,考查分层抽样、频率、概率、期望的计算公式.第一问,利用频率=高×组距计算后三组的频率;第二问,①先计算出第三组的总人数30人,第三组需抽取3人,再计算概率;②先用分层抽样计算出每组中分别抽取多少人,分别计算每种情况的概率,再画出分布列求期望.
试题解析:(1) 解:
第三组的频率为0.06 5=0.3;
5=0.3;
第四组的频率为0.04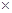 5=0.2;
5=0.2;
第五组的频率为0.02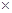 5=0.1 3分
5=0.1 3分
(2)解:
① 设学生甲和学生乙同时进入第二轮面试的事件为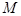
则 6分
6分
②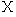 的可能取
的可能取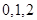 ,抽取的6人中,第3,4,5组人数分别为3,2,1人
,抽取的6人中,第3,4,5组人数分别为3,2,1人

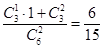
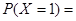
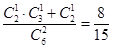
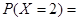
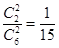 10分
10分
|
X |
0 |
1 |
2 |
|
P |
|
|
|
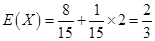 13分
13分
考点:1.频率分步直方图;2.分层抽样;3.分布列;4.期望.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
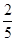
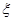 名学生被考官D面试,求
名学生被考官D面试,求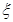 名学生被考官D面试,求
名学生被考官D面试,求