题目内容
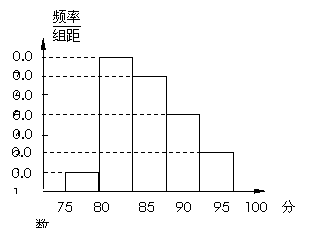
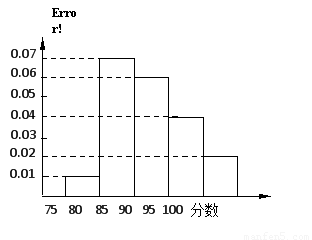
某高校在2012年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
(1)分别求第3,4,5组的频率;
(2) 若该校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试。
(ⅰ) 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙恰有一人进入第二轮面试的概率;
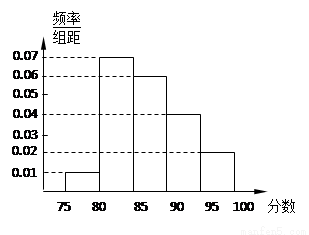
(ⅱ) 学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官L的面试,设第4组中有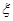 名学生被考官L面试,求
名学生被考官L面试,求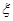 的分布列和数学期望.
的分布列和数学期望.

【答案】
(1) 第三组的频率为0.06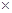 5=0.3; 第四组的频率为0.04
5=0.3; 第四组的频率为0.04 5=0.2;
5=0.2;
第五组的频率为0.02 5=0.1.
……………………3分
5=0.1.
……………………3分
(2)(ⅰ)设“学生甲和学生乙恰有一人进入第二轮面试”为事件A,第三组应有3人进入面试
则: P(A)= 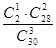
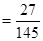 ……………………6分
……………………6分
(ⅱ)第四组应有2人进入面试,则随机变量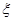 可能的取值为0,1,2.
…………7分
可能的取值为0,1,2.
…………7分
且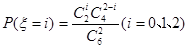 ,则随机变量
,则随机变量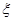 的分布列为:
的分布列为:
|
|
0 |
1 |
2 |
|
P |
|
|
|
……………………10分
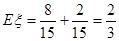
【解析】略

练习册系列答案
相关题目
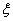
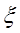 名学生被考官L面试,求
名学生被考官L面试,求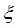 的分布列和数学期望.
的分布列和数学期望.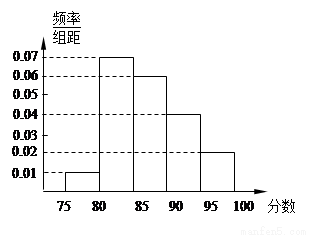
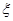 名学生被考官L面试,求
名学生被考官L面试,求