题目内容
如图,在平面直角坐标系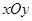 中,
中,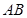 是半圆
是半圆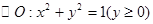 的直径,
的直径,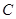 是半圆
是半圆 (除端点
(除端点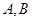 )上的任意一点.在线段
)上的任意一点.在线段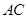 的延长线上取点
的延长线上取点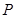 ,使
,使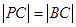 ,试求动点
,试求动点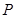 的轨迹方程
的轨迹方程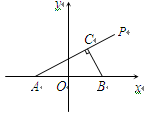
点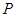 的轨迹方程为
的轨迹方程为
解析试题分析:[解法一]连结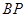 ,由已知可得
,由已知可得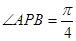 ,
,
∴ 点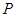 在以
在以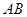 为弦,所对圆周角为
为弦,所对圆周角为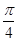 的圆上.
的圆上.
设该圆的圆心为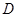 ,则点
,则点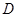 在弦
在弦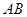 的中垂线上,即
的中垂线上,即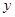 轴上,且
轴上,且 ,
,
∴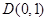 ,
,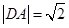 .圆
.圆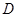 的方程为
的方程为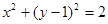 .
.
当点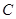 趋近于点
趋近于点 时,点
时,点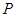 趋近于点
趋近于点 ;当点
;当点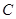 趋近于点
趋近于点 时,点
时,点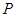 趋近于点
趋近于点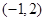 .
.
所以点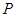 的轨迹方程为
的轨迹方程为
[解法二] 连结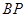 ,由已知可得
,由已知可得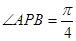 ,
,
设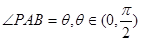 ,则
,则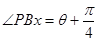
故若设直线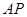 的斜率为
的斜率为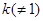 时,直线
时,直线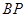 的斜率为
的斜率为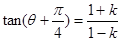 .
.
故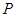 为两直线
为两直线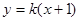 及
及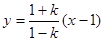 的交点,消去
的交点,消去 得
得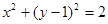 ,当
,当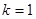 时,
时,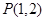 也在该圆上.
也在该圆上.
结合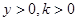 可知,点
可知,点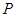 的轨迹方程为
的轨迹方程为
考点:本试题考查了点的轨迹方程的求解。
点评:解决该试题的关键是建立动点满足的关系式,设出点的坐标,建立关系式,将关系式坐标化,然后化简得到其轨迹方程,一般来说,先考虑运用定义法求解轨迹,再考虑运用直接法来求解,中档题。

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 为抛物线
为抛物线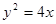 的焦点,
的焦点,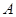 为抛物线上任意一点,已
为抛物线上任意一点,已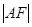 为半径画圆,与
为半径画圆,与 轴负半轴交于
轴负半轴交于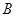 点,试判断过
点,试判断过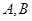 的直线与抛物线的位置关系,并证明。
的直线与抛物线的位置关系,并证明。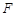 为抛物线
为抛物线 :
: 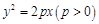 的焦点,
的焦点, 为抛物线
为抛物线 .
.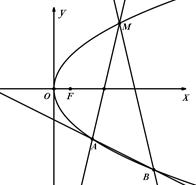
 的坐标;
的坐标;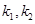 的两直线
的两直线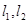 ,
, 与抛物线
与抛物线 ,
, 与抛物线
与抛物线 ,记直线
,记直线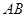 的斜率为
的斜率为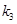 .
. ,试求
,试求 为定值.
为定值.
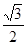 。
。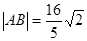 ,求直线l的方程。
,求直线l的方程。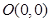 的距离是到定点
的距离是到定点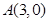 距离的二倍,求这条曲线的方程.
距离的二倍,求这条曲线的方程.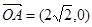 ,
,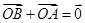 ,O为坐标原点,动点E满足:
,O为坐标原点,动点E满足: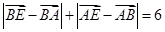
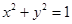 引两条切线PA、PB,切点分别为A、B,直线AB与x轴、y轴分别交于M、N两点,求ΔMON面积的最小值.
引两条切线PA、PB,切点分别为A、B,直线AB与x轴、y轴分别交于M、N两点,求ΔMON面积的最小值.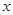 轴对称,它的顶点在坐标原点,并且经过点
轴对称,它的顶点在坐标原点,并且经过点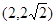
 过抛物线的焦点F,与抛物线交于A、B两点,线段AB的中点M的横坐标为3,求弦长
过抛物线的焦点F,与抛物线交于A、B两点,线段AB的中点M的横坐标为3,求弦长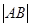 以及直线
以及直线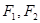 分别为椭圆
分别为椭圆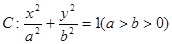 的左、右焦点,点
的左、右焦点,点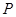 为椭圆上任意一点,
为椭圆上任意一点,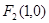 的距离的最大值为
的距离的最大值为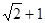 .
.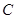 的方程。
的方程。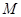 的坐标为
的坐标为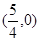 ,过点
,过点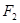 且斜率为
且斜率为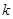 的直线
的直线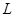 与椭圆
与椭圆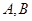 两点。对于任意的
两点。对于任意的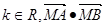 是否为定值?若是求出这个定值;若不是说明理由。
是否为定值?若是求出这个定值;若不是说明理由。