题目内容
已知抛物线C关于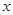 轴对称,它的顶点在坐标原点,并且经过点
轴对称,它的顶点在坐标原点,并且经过点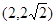
(1)求抛物线C的标准方程
(2)直线 过抛物线的焦点F,与抛物线交于A、B两点,线段AB的中点M的横坐标为3,求弦长
过抛物线的焦点F,与抛物线交于A、B两点,线段AB的中点M的横坐标为3,求弦长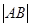 以及直线
以及直线 的方程。
的方程。
(1) ;(2)直线
;(2)直线 方程为:
方程为: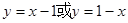 ;
;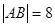 .
.
解析试题分析:(1)依题意设抛物线方程为: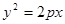 过
过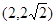 得
得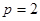
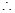 抛物线方程为
抛物线方程为 ……4分
……4分
(2)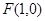 令
令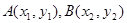
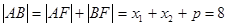
当直线 斜率不存在时即方程为:
斜率不存在时即方程为: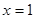 此时AB中点为F(1,0)不合题意,舍去 ……6分
此时AB中点为F(1,0)不合题意,舍去 ……6分
令直线 方程为:
方程为: 代入抛物线方程得:
代入抛物线方程得: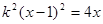
得: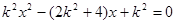 ……9分
……9分
得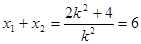 得
得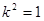 ,
,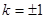
直线 方程为:
方程为: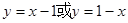 ;
;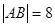 ……13分
……13分
考点:本题考查了抛物线方程的求法及直线与抛物线的位置关系。
点评:对于弦长问题,只需联立方程利用韦达定理及弦长公式求解即可。

练习册系列答案
相关题目
 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 点在
点在 上,
上,  点在
点在 上,且对角线
上,且对角线 过点
过点 ,已知
,已知 米,
米,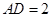 米.
米. 的长应在什么范围内?
的长应在什么范围内?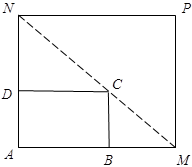
 中,
中, 是半圆
是半圆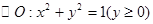 的直径,
的直径,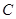 是半圆
是半圆 (除端点
(除端点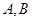 )上的任意一点.在线段
)上的任意一点.在线段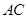 的延长线上取点
的延长线上取点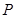 ,使
,使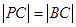 ,试求动点
,试求动点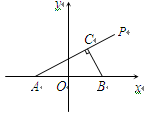
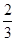 ,焦点在x轴上的椭圆;
,焦点在x轴上的椭圆;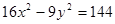 的左顶点.
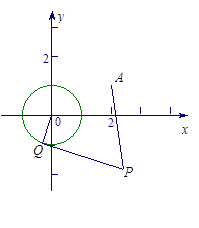
的左顶点.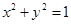 和定点A(2,1),由圆O外一点
和定点A(2,1),由圆O外一点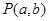 向圆O引切线PQ,切点为Q,且满足
向圆O引切线PQ,切点为Q,且满足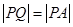
 中,两个定点
中,两个定点 ,
, 交动点C的轨迹于P、Q两点,求
交动点C的轨迹于P、Q两点,求 面积的最大值(O是坐标原点)。
面积的最大值(O是坐标原点)。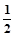
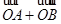 与
与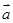 =(3,-1)共线.
=(3,-1)共线.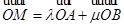 (
(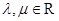 ),证明
),证明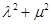 为定值.
为定值.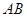 、
、 分别是圆
分别是圆 和椭圆
和椭圆 的弦,且弦的端点在
的弦,且弦的端点在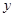 轴的异侧,端点
轴的异侧,端点 与
与 、
、 与
与 的横坐标分别相等,纵坐标分别同号.
的横坐标分别相等,纵坐标分别同号.
 ,且弦
,且弦 ,求直线
,求直线 ,试探究弦
,试探究弦