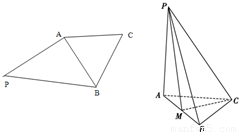
题目内容
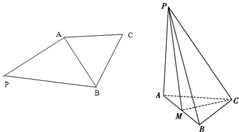 如图所示,平面四边形PABC中,∠PAB为直角,△ABC为等边三角形,现把△PAB沿着AB折起,使得△APB与△ABC垂直,且点M为AB的中点.
如图所示,平面四边形PABC中,∠PAB为直角,△ABC为等边三角形,现把△PAB沿着AB折起,使得△APB与△ABC垂直,且点M为AB的中点.(1)求证:平面PAB⊥平面PCM
(2)若2PA=AB,求直线BC与平面PMC所成角的余弦值.
分析:(1)由面APB⊥面ABC,PA⊥AB,得到线PA⊥面ABC,从而得到PA⊥CM,根据M为等边三角形ABC的中点,得到CM⊥AB,从而证出线面垂直,进一步得到面面垂直;
(2)求直线BC与平面PMC所成角的余弦值,首先利用等积法求出B到面PMC的距离,该距离与BC长度的比值为直线BC与平面PMC所成角的正弦值,利用同角三角函数的基本关系式求出余弦值.
(2)求直线BC与平面PMC所成角的余弦值,首先利用等积法求出B到面PMC的距离,该距离与BC长度的比值为直线BC与平面PMC所成角的正弦值,利用同角三角函数的基本关系式求出余弦值.
解答:(1)证明:∵△APB⊥△ABC且交线为AB
又∵∠PAB为直角,所以AP⊥平面ABC,
故AP⊥CM,
又∵△ABC为等边三角形,点M为AB的中点,
所以CM⊥AB,又∵PA∩AB=A
所以CM⊥平面PAB,又CM?△ABC
所以平面PAB⊥平面PCM;
(2)解:假设PA=a,则AB=2a,再设B到平面PMC的距离为hB.
则VP-MBC=VB-PMC=
PA•SMBC=
hB•SPMC
在直角三角形PAM中,由PA=AM=a,得PM=
a,
在等边三角形ABC中,AB边上的高CM=
a,
而三角形PMC为直角三角形,
故面积为S△PMC=
CM•PM=
•
a•
a=
a2.
又S△MBC=
S△ABC=
a2.
∴a•
a2=hB•
a2.
故hB=
a
所以直线BC与平面PMC所成角的正弦值sinθ=
=
=
.
所以余弦值为cosθ=
=
=
.
又∵∠PAB为直角,所以AP⊥平面ABC,
故AP⊥CM,
又∵△ABC为等边三角形,点M为AB的中点,
所以CM⊥AB,又∵PA∩AB=A
所以CM⊥平面PAB,又CM?△ABC
所以平面PAB⊥平面PCM;
(2)解:假设PA=a,则AB=2a,再设B到平面PMC的距离为hB.
则VP-MBC=VB-PMC=
| 1 |
| 3 |
| 1 |
| 3 |
在直角三角形PAM中,由PA=AM=a,得PM=
| 2 |
在等边三角形ABC中,AB边上的高CM=
| 3 |
而三角形PMC为直角三角形,
故面积为S△PMC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
又S△MBC=
| 1 |
| 2 |
| ||
| 2 |
∴a•
| ||
| 2 |
| ||
| 2 |
故hB=
| ||
| 2 |
所以直线BC与平面PMC所成角的正弦值sinθ=
| hB |
| BC |
| ||||
| 2a |
| ||
| 4 |
所以余弦值为cosθ=
| 1-sin2θ |
1-(
|
| ||
| 4 |
点评:本题考查了面面垂直的判定,考查了直线和平面所成的角,训练了等积法,求解直线和平面所成角,可通过求平面的斜线上的点到平面的距离,然后用点到平面的距离比上该点到斜足的距离得到线面角的正弦值.此题是中档题.

练习册系列答案
相关题目
 如图所示,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图所示,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC

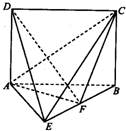 已知几何体E-ABCD如图所示,其中四边形ABCD为矩形,△ABE为等边三角形,且
已知几何体E-ABCD如图所示,其中四边形ABCD为矩形,△ABE为等边三角形,且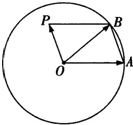 已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足
已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足