题目内容

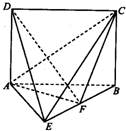已知几何体E-ABCD如图所示，其中四边形ABCD为矩形，△ABE为等边三角形，且AD=
3
，AE=2，DE=
7
，点F为棱BE上的动点．
（I）若DE∥平面AFC，试确定点F的位置；
（II）在（I）条件下，求几何体D-FAC的体积．
分析：（I）连接BD交AC于点M，若DE∥平面AFC，则DE∥FM，点M为BD中点，则F为棱BE的中点即可确定点F的位置；
（II）在（I）条件下，求出底面DAC的面积，求出F到底面的距离，即可求几何体D-FAC的体积．
解答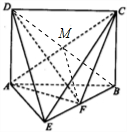：解：（I）证明：连接BD交AC于点M，若DE∥平面AFC，因为平面AFC∩平面BDE=MF，
则DE∥FM，点M为BD中点，则F为棱BE的中点…（6分）
（II）因为VD-FAC=VF-ACD=
1
3
S△ACD•
3
2
=
1
2

所求体积为
1
2
．…（12分）
点评：本题是中档题，考查几何体的体积的求法，转化思想的应用，直线与平面平行的应用，考查空间想象能力．
练习册系列答案
相关题目
精英家教网如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．
（Ⅰ）证明EF∥平面PAB；
（Ⅱ）证明EF⊥平面PBC；
（III）点M是四边形ABCD内的一动点，PM与平面ABCD所成的角始终为45°，求动直线PM所形成的曲面与平面ABCD、平面PAB、平面PAD所围成几何体的体积．
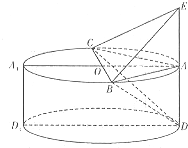如图，一个几何体由圆柱ADD1A1和三棱锥E-ABC组合而成，点A，B，C在⊙O的圆周上，E，A，D三点共线，已知AB⊥AC，AB=AC，AE=AD=1，BC=2．
（1）求证：AC⊥BD；
（2）求三棱锥C-BDE的体积．
给出下列命题：
①已知函数f(x)=(
1
2x-1
)•x2-sinx+a(a为常数)，且f（loga1000）=3，则f（lglg2）=3；
②若函数f（x）=lg（x2+ax-a）的值域是R，则a∈（-4，0）；
③关于x的方程(
1
2
)x=lga有非负实数根，则实数a的取值范围是（1，10）；
④如图，三棱柱ABC-A1B1C1中，E、F分别是AB，AC的中点，平面EB1C1F将三棱柱分成几何体AEF-AB1C1和B1C1-EFCB两部分，其体积分别为V1，V2，则V1：V2=7：5．
其中正确命题的序号是
①③④
①③④
．
精英家教网如图，已知，在空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点．
（1）求证：平面CDE⊥平面ABC；
（2）若AB=DC=3，BC=5，BD=4，求几何体ABCD的体积；
（3）若G为△ADC的重心，试在线段AB上找一点F，使得GF∥平面CDE．
（2011•顺义区一模）如图，已知在空间四边形ABCD中，AB=AC=DB=DC，E为BC的中点．
（Ⅰ）求证：平面ADE⊥平面ABC；
（Ⅱ）若AB=5，BC=6，AD=4，求几何体ABCD的体积；
（Ⅲ）在（Ⅱ）的条件下，若G为△ABD的重心，试问在线段BC上是否存在点F，使GF∥平面ADE？若存在，请指出点F在BC上的位置，若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网