题目内容
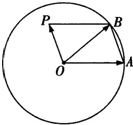 已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足
已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足| OP |
| OA |
| OB |
(1)如图所示,若四边形OABP为平行四边形,求m的值;
(2)若m=2,求|
| OP |
(3)若
| OA |
| OB |
| 1 |
| 3 |
| OD |
| OA |
分析:(1)利用向量的减法运算,结合条件,即可得到结论;
(2)利用向量的加法运算,可得结论;
(3)分类讨论,利用向量的数量积运算,可得结论.
(2)利用向量的加法运算,可得结论;
(3)分类讨论,利用向量的数量积运算,可得结论.
解答:解:(1)由题意,
=
=
-

∵
=m
+
,∴m=-1;
(2)m=2,
=2
+
∵单位圆O上的两点A,B及单位圆所在平面上的一点P,
∴1<|
|<3;
(3)因为
•
=-
,所以cos∠BOA=-
所以cos∠BAO=cos∠ABO=
所以
•
=m-
所以①当∠OPB=90°时,∠POA=90°,所以
•
=0;
②当∠POB=90°时,因为cos∠BAO=cos∠ABO=
,所以tan∠OBA=
所以OD=
又因为cos∠BOA=-
,∠BOA-∠DOA=90°,所以cos∠DOA=
所以
•
=
.
| OP |
| AB |
| OB |
| OA |

∵
| OP |
| OA |
| OB |
(2)m=2,
| OP |
| OA |
| OB |
∵单位圆O上的两点A,B及单位圆所在平面上的一点P,
∴1<|
| OP |
(3)因为
| OA |
| OB |
| 1 |
| 3 |
| 1 |
| 3 |
所以cos∠BAO=cos∠ABO=
| ||
| 3 |
所以
| OP |
| OA |
| 1 |
| 3 |
所以①当∠OPB=90°时,∠POA=90°,所以
| OD |
| OA |
②当∠POB=90°时,因为cos∠BAO=cos∠ABO=
| ||
| 3 |
| ||
| 2 |
所以OD=
| ||
| 2 |
又因为cos∠BOA=-
| 1 |
| 3 |
2
| ||
| 3 |
所以
| OD |
| OA |
| 2 |
| 3 |
点评:本题考查向量的运算,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
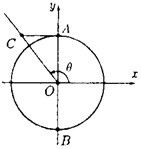 如图,已知单位圆O与y轴相交于A、B两点.角θ的顶点为原点,始边在x轴的正半轴上,终边在射线OC上.过点A作直线AC垂直于y轴且与角θ的终边交于点C,则有向线段AC的函数值是( )
如图,已知单位圆O与y轴相交于A、B两点.角θ的顶点为原点,始边在x轴的正半轴上,终边在射线OC上.过点A作直线AC垂直于y轴且与角θ的终边交于点C,则有向线段AC的函数值是( )| A、sinθ | B、cosθ | C、tanθ | D、cotθ |
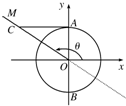 如图所示,已知单位圆O与y轴交于A、B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么?
如图所示,已知单位圆O与y轴交于A、B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么?
