题目内容
如图所示，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD=∠FAB=90°，BC
| 1 |
| 2 |
| 1 |
| 2 |
分析：利用同一法，证明直线CD，EF相交，即可得到结论．
解答：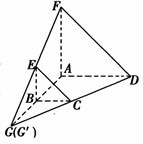
证明：延长DC交AB的延长线于点G，则
∵BC∥AD，BC=
AD，
∴
=
=
=
延长FE交AB的延长线于G′，同理可得
=
=
=
∴
=
∴G与G′重合
∴直线CD，EF相交于点G，即C，D，F，E四点共面．
证明：延长DC交AB的延长线于点G，则∵BC∥AD，BC=
| 1 |
| 2 |
∴
| GB |
| GA |
| GC |
| GD |
| BC |
| AD |
| 1 |
| 2 |
延长FE交AB的延长线于G′，同理可得
| G′E |
| G′F |
| G′B |
| G′A |
| BE |
| AF |
| 1 |
| 2 |
∴
| G′B |
| G′A |
| GB |
| GA |
∴G与G′重合
∴直线CD，EF相交于点G，即C，D，F，E四点共面．
点评：本题考查平面的基本性质，考查同一法，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
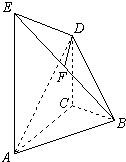在如图所示的几何体中，AE⊥平面ABC，CD∥AE，F是BE的中点，AC=BC=1，∠ACB=90°，AE=2CD=2．
如图所示，在四凌锥E-ABCD中，AD⊥平面ABE，四边形ABCD为矩形，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE，AC∩BD=G．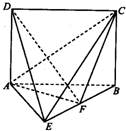
已知几何体E-ABCD如图所示，其中四边形ABCD为矩形，△ABE为等边三角形，且
如图所示，矩形ABCD中，AD⊥平面ABE，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE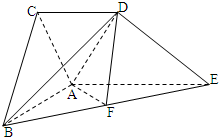
在如图所示的几何体中，△ABC为正三角形，AE和CD都垂直于平面ABC，且AE=AB=2，CD=1，F为BE的中点．