题目内容
【题目】已知函数![]() (
(![]() )的图象过点
)的图象过点![]() ,
,![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求![]() ;
;
(3)解方程![]() .
.
【答案】(1)f(x)=4﹣2x(2)﹣5(3)![]()
【解析】
(1)根据f(x)的图象过点A、B两点,求出b、a的值,得f(x)的解析式;
(2)由f(x)的解析式求出f(log481)的值;
(3)由f(x)的解析式化简方程f(2x)=﹣21,求出解来即可.
解:(1)∵f(x)=a﹣bx(b>0)的图象过点A(2,0),B(1,2),
∴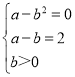
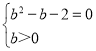
解得b=2,a=4;
∴函数f(x)=4﹣2x;
(2)∵f(x)=4﹣2x,
∴f(log481)=4![]()
=4![]()
=4﹣9
=﹣5;
(3)∵f(x)=4﹣2x,
∴方程f(2x)=﹣21可化为
4﹣22x=﹣21,
即4+21=22x,
∴22x=25,
∴2x=5,
解得x=log25.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
