题目内容
设向量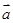 与
与 的夹角为
的夹角为 ,
,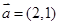 ,
,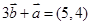 ,则
,则 ________.
________.
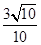
解析试题分析:设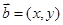 ,则由
,则由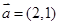 ,
,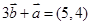 可得
可得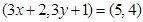 ,即
,即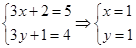 ,所以
,所以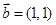 ,故
,故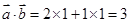 且
且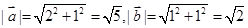 ,所以
,所以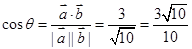 .
.
考点:1.平面向量的坐标运算;2.平面向量的数量积.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
题目内容
设向量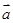 与
与 的夹角为
的夹角为 ,
,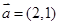 ,
,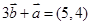 ,则
,则 ________.
________.
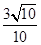
解析试题分析:设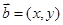 ,则由
,则由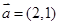 ,
,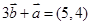 可得
可得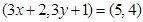 ,即
,即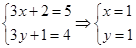 ,所以
,所以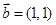 ,故
,故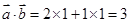 且
且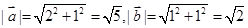 ,所以
,所以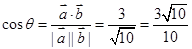 .
.
考点:1.平面向量的坐标运算;2.平面向量的数量积.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案