题目内容
(文科)(本题满分14分)设函数f(x)= ·
· ,其中
,其中 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点(
=(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点( ,2).
,2).
(Ⅰ)求实数m的值;
(Ⅱ)求函数f(x)的最小值及此时x值的集合
(理科)(本题满分14分)已 知函数f(x)=ex-kx,x∈R
知函数f(x)=ex-kx,x∈R
(Ⅰ)若k=e,试确定函数f(x)的单调区间
(Ⅱ)若k>0,且对于任意x∈R,f(|x|)>0恒成立,试确定实数k的取值范围
(文科)解:(Ⅰ)f(x)=a·b="m(1+sin2x)+cos2x."
由已知得f( )=m(1+sin
)=m(1+sin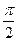 )+cos
)+cos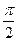 =2,解得m=1.……6分
=2,解得m=1.……6分
(Ⅱ)由(Ⅰ)得f( x)=1+sin2x+cos2x=1+
x)=1+sin2x+cos2x=1+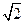 sin(2x+
sin(2x+ ).
).
所以当sin(2x+ )=-1时,f(x)的最小值为1-
)=-1时,f(x)的最小值为1-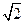 . ……………11分
. ……………11分
由sin(2x+ )=-1,得x值的集合为{x|x=k
)=-1,得x值的集合为{x|x=k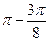 ,k∈Z}.……14分
,k∈Z}.……14分
(理科)解:(Ⅰ)由k=e得f(x)=ex-ex,所以f (x)=ex-e.
(x)=ex-e.
由f (x)>0得x>1,
(x)>0得x>1,
故f(x)的单调递增区间是(1,+∞);……………………4分
由f (x)<0得x<1,
(x)<0得x<1,
故f(x)的单调递减区间是(-∞,1). ……………………6分
(Ⅱ)由f(|-x|)=f(|x|)可知f(|x|)是偶函数. 于是 f(|x|)>0对任意x∈R成立等价于f(x)>0对任意x≥0成立. 由f
f(|x|)>0对任意x∈R成立等价于f(x)>0对任意x≥0成立. 由f (x)=ex-k=0得x="lnk."
(x)=ex-k=0得x="lnk."
①当k∈(0,1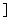 时,f
时,f (x)=ex-k>1-k≥0(x>0). 此时f(x)在[0,+∞
(x)=ex-k>1-k≥0(x>0). 此时f(x)在[0,+∞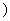 上单调递增. 故f(x)≥f(0)=1>0,符合题意.所以0<k≤1. …………10分②当k∈(1,+∞)时,lnk>0. 当x变化时f
上单调递增. 故f(x)≥f(0)=1>0,符合题意.所以0<k≤1. …………10分②当k∈(1,+∞)时,lnk>0. 当x变化时f (x),f(x)的变化情况如下
(x),f(x)的变化情况如下 :
:
由此可得,在[0,+∞x (0,lnk) lnk (lnk,+∞) f  (x)
(x)- 0 + f(x) 单调递减 极小值 单调递增 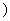 上,f(x)≥f(lnk)=k-klnk.
上,f(x)≥f(lnk)=k-klnk.
依题意,k-klnk>0. 又k>1,所以1<k<e.
综合①②实数k的取值范围为(0,e). …………………………14分
解析

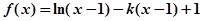 .
.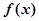 的单调区间;
的单调区间;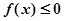 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;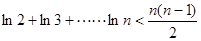
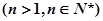 .
.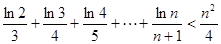
 ·
· ,其中
,其中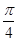 ,2).
,2). .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.