题目内容
(文科)(本题满分14分)设函数f(x)=![]() ·
·![]() ,其中
,其中![]() =(m,cos2x),
=(m,cos2x),![]() =(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点(
=(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点(![]() ,2).
,2).
(Ⅰ)求实数m的值;
(Ⅱ)求函数f(x)的最小值及此时x值的集合.
(文科)解:(Ⅰ)f(x)=a·b=m(1+sin2x)+cos2x.
由已知得f(![]() )=m(1+sin
)=m(1+sin![]() )+cos
)+cos![]() =2,解得m=1.……6分
=2,解得m=1.……6分
(Ⅱ)由(Ⅰ)得f(x)=1+sin2x+cos2x=1+![]() sin(2x+
sin(2x+![]() ).
).
所以当sin(2x+![]() )=-1时,f(x)的最小值为1-
)=-1时,f(x)的最小值为1-![]() . ……………11分
. ……………11分
由sin(2x+![]() )=-1,得x值的集合为{x|x=k
)=-1,得x值的集合为{x|x=k![]() ,k∈Z}.……14分
,k∈Z}.……14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ·
· ,其中
,其中 ,2).
,2). 知函数f(x)=ex-kx,x∈R
知函数f(x)=ex-kx,x∈R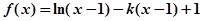 .
. 的单调区间;
的单调区间;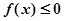 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;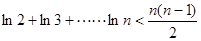
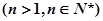 .
.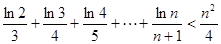
 ·
· ,其中
,其中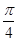 ,2).
,2). .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.