题目内容
(本题满分14分)已知函数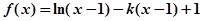 .
.
(1)求函数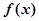 的单调区间;
的单调区间;
(2)若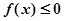 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(文科(3)证明: 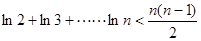
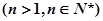 .
.
(理科(3)证明: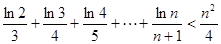
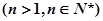 .
.
【答案】
(1)当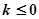 时,函数
时,函数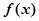 的递增区间为
的递增区间为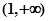 ,………2分
,………2分
当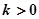 时,函数
时,函数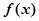 的递增区间为
的递增区间为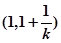 ,减区间为
,减区间为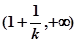
(2)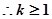 (3)见解析
(3)见解析
【解析】(1)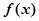 的定义域为
的定义域为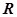 ,
,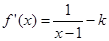 ,………1分
,………1分
当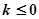 时,函数
时,函数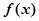 的递增区间为
的递增区间为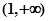 ,………2分
,………2分
当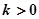 时,函数
时,函数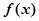 的递增区间为
的递增区间为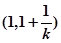 ,减区间为
,减区间为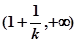 .………4分
.………4分
(2)由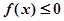 得
得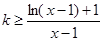 ,………5分
,………5分
令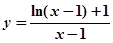 ,则
,则 ………6分
………6分
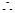 当
当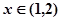 时
时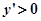 ,函数递增;当
,函数递增;当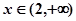 时
时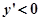 ,函数递减。………8分
,函数递减。………8分
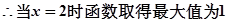 ,
,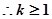 ………10分
………10分
(3)由(1)可知若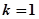 ,当
,当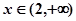 时有
时有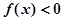 ,………11分
,………11分
即有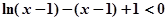 ,即
,即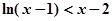 ,即有
,即有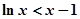 (x>1), ………12
(x>1), ………12
(文)令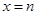 ,则
,则 ,
,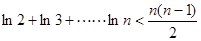 ,………14
,………14
(理)令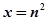 ,则
,则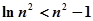 ,
,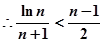 ,………13分
,………13分
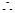
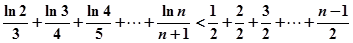 =
=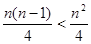 (n>1)
(n>1)
思路分析:(1)先求出函数的定义域,求函数的导数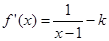 ,讨论分别求出函数
,讨论分别求出函数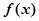 的单调区间;
的单调区间;
(2)分离参数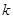 求出函数
求出函数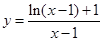 的最大值即可;
的最大值即可;
(3)由(1)得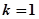 时,
时,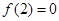 ,所以
,所以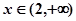 时有
时有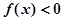 ,即有
,即有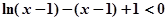 ,可得
,可得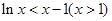 ,令
,令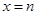 ,则
,则 ,
,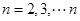
左右分别相加可证出文科的结论;理科令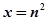 ,求和再放缩可得结论。
,求和再放缩可得结论。

练习册系列答案
相关题目

 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
