题目内容
已知f（x）是周期为2的奇函数，且当x∈（0，1）时，f（x）=2x，则f（log0.57）=分析：由f（x）是周期为2的奇函数，我们易根据-2＞log0.57＞-3，得到f（log0.57）=f（log0.5
），再由当x∈（0，1）时，f（x）=2x，我们结合对数运算性质我们易得结果．
| 7 |
| 16 |
解答：解：∵4＜7＜8
而y=log0.5x为函数
∴log0.54＞log0.57＞log0.58
∴-2＞log0.57＞-3
f（log0.57）=f（log0.57+2×2）
=f（log0.5
）=2log0.5
=
故答案：
而y=log0.5x为函数
∴log0.54＞log0.57＞log0.58
∴-2＞log0.57＞-3
f（log0.57）=f（log0.57+2×2）
=f（log0.5
| 7 |
| 16 |
| 7 |
| 16 |
| 16 |
| 7 |
故答案：
| 16 |
| 7 |
点评：本题考查的知识点是对数的运算性质，及函数的周期性，对数运算中的alogaN=N（N＞0）是解答的关键．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知f（x）是周期为2的奇函数，当0＜x＜1时，f（x）=lgx．设a=f(
)，b=f(
)，c=f(
)，则（ ）
| 6 |
| 5 |
| 3 |
| 2 |
| 5 |
| 2 |
| A、a＜b＜c |
| B、b＜a＜c |
| C、c＜b＜a |
| D、c＜a＜b |
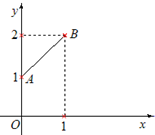已知f（x）是周期为2的偶函数．当0≤x≤1时，f（x）的图象是如图中的线段AB，那么