题目内容
已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx.设a=f(
),b=f(
),c=f(
),则( )
| 6 |
| 5 |
| 3 |
| 2 |
| 5 |
| 2 |
| A、a<b<c |
| B、b<a<c |
| C、c<b<a |
| D、c<a<b |
分析:首先利用奇函数的性质与函数的周期性把f(x)的自变量转化到区间(0,1)内,然后由对数函数f(x)=lgx的单调性解决问题.
解答:解:已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx.
则a=f(
)=f(-
)=-f(
)=-lg
>0,
b=f(
)=f(-
)=-f(
)=-lg
>0,
c=f(
)=f(
)=lg
<0,
又lg
>lg
∴0<-lg
<-lg
∴c<a<b,
故选D.
则a=f(
| 6 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
b=f(
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
c=f(
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又lg
| 4 |
| 5 |
| 1 |
| 2 |
∴0<-lg
| 4 |
| 5 |
| 1 |
| 2 |
∴c<a<b,
故选D.
点评:本题主要考查奇函数性质与函数的周期性,同时考查对数函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
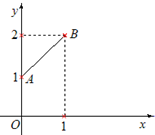 已知f(x)是周期为2的偶函数.当0≤x≤1时,f(x)的图象是如图中的线段AB,那么
已知f(x)是周期为2的偶函数.当0≤x≤1时,f(x)的图象是如图中的线段AB,那么