题目内容
在极坐标系中，曲线C1方程为ρ=2sin（θ+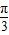
），曲线C2：方程为ρsin（θ+
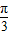）=4．以极点O为原点，极轴方向为x轴正向建立直角坐标系xOy．（1）求曲线C1，C2的直角坐标方程；
（2）设A、B分别是C1，C2上的动点，求|AB|的最小值．
【答案】分析：（1）先将曲线C1及曲线C2的极坐标方程展开，然后再利用公式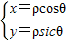
，即可把极坐标方程化为普通方程．
（2）可先求出圆心到直线的距离，再减去其半径即为所求的最小值．
解答：解：（Ⅰ）曲线C1的极坐标方程化为ρ=sinθ+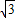
cosθ，
两边同乘以ρ，得ρ2=ρsinθ+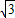
ρcosθ，
则曲线C1的直角坐标方程为x2+y2=y+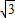
x，即x2+y2-
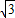x-y=0．
曲线C2的极坐标方程化为
ρsinθ+
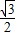ρcosθ=4，
则曲线C2的直角坐标方程为
y+
x=4，即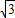
x+y-8=0．
（Ⅱ）将曲线C1的直角坐标方程化为（x-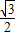
）2+（y-
）2=1，
它表示以（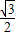
，
）为圆心，以1为半径的圆．
该圆圆心到曲线C2即直线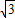
x+y-8=0的距离
d=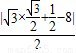
=3，
所以|AB|的最小值为3-1=2．
点评：掌握极坐标方程化为普通方程的公式和点到直线的距离公式及转化思想是解题的关键．
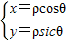，即可把极坐标方程化为普通方程．（2）可先求出圆心到直线的距离，再减去其半径即为所求的最小值．
解答：解：（Ⅰ）曲线C1的极坐标方程化为ρ=sinθ+
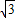cosθ，两边同乘以ρ，得ρ2=ρsinθ+
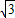ρcosθ，则曲线C1的直角坐标方程为x2+y2=y+
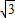x，即x2+y2-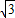x-y=0．曲线C2的极坐标方程化为
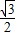ρsinθ+ρcosθ=4，则曲线C2的直角坐标方程为
y+x=4，即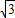x+y-8=0．（Ⅱ）将曲线C1的直角坐标方程化为（x-
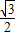）2+（y-）2=1，它表示以（
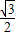，）为圆心，以1为半径的圆．该圆圆心到曲线C2即直线
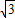x+y-8=0的距离d=
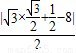=3，所以|AB|的最小值为3-1=2．
点评：掌握极坐标方程化为普通方程的公式和点到直线的距离公式及转化思想是解题的关键．
练习册系列答案
相关题目
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分，请在答题纸指定区域内作答，解答应写出文字说明、证明过程或演算步骤．