题目内容
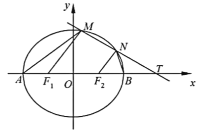
【题目】已知椭圆![]() 的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,
的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)设点![]() 在椭圆
在椭圆![]() 上运动,
上运动,![]() ,且点
,且点![]() 到直线
到直线![]() 的距离为常数
的距离为常数![]() ,求动点
,求动点![]() 的轨迹方程.
的轨迹方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由椭圆的右焦点与短轴两端点构成一个面积为![]() 的等腰直角三角形,求出
的等腰直角三角形,求出![]() ,可得椭圆方程;(2)设
,可得椭圆方程;(2)设![]() ,则
,则![]() 的方程为:
的方程为:![]() ,由
,由![]() 得
得![]() 点坐标,可证明
点坐标,可证明![]() .(3) 设
.(3) 设![]() ,由
,由![]() 得
得![]() ,又
,又![]() 点在椭圆上得:
点在椭圆上得:![]() ,从而
,从而![]()
![]() 化简可得
化简可得![]() 的轨迹方程.
的轨迹方程.
试题解析:
解:(1)由条件可得![]() ,
,![]()
椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,则
,则![]() 的方程为:
的方程为:![]() ,
,
由![]() 得:
得:![]()
所以
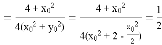 .
.
(3)设![]() ,由
,由![]() 得
得![]() ①
①
又![]() 点在椭圆上得:
点在椭圆上得:![]() ②
②
联立①②可得![]() ,
,![]() ③
③
由![]() 得
得![]() ,
,
即![]()
可得![]() ,
,
将③代入得:

化简得![]() 点轨迹方程为:
点轨迹方程为:![]() .
.
点睛:本题考查圆锥曲线的标准方程,曲线与方程,直线与椭圆的位置关系以及定值问题,属于中档题目.证明定值问题,先设出![]() 点坐标,根据
点坐标,根据![]() 求出直线
求出直线![]() 的方程,再根据
的方程,再根据![]() 点在
点在![]() 上求出坐标, 证明
上求出坐标, 证明![]() 为定值,利用两点间距离公式代入坐标,根据点在曲线上两元换一元,分子分母成倍数关系,即为定值.
为定值,利用两点间距离公式代入坐标,根据点在曲线上两元换一元,分子分母成倍数关系,即为定值.

练习册系列答案
相关题目
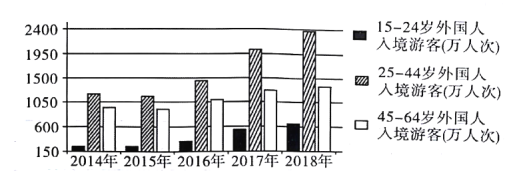
【题目】当前,旅游已经成为新时期人民群众美好生活和精神文化需求的重要内容.旅游是综合性产业,是拉动经济发展的重要动力,也为整个经济结构调整注入活力.文化旅游产业研究院发布了《2019年中国文旅产业发展趋势报告》,报告指出:旅游业稳步增长,每年占国家GDP总量的比例逐年增加,如图及下表为2014年到2018年的相关统计数据.
旅游收入占国家GDP总量比例趋势 | |||||
年份: | 1 | 2 | 3 | 4 | 5 |
占比: | 10.4 | 10.8 | 11.0 | 11.0 | 11.2 |
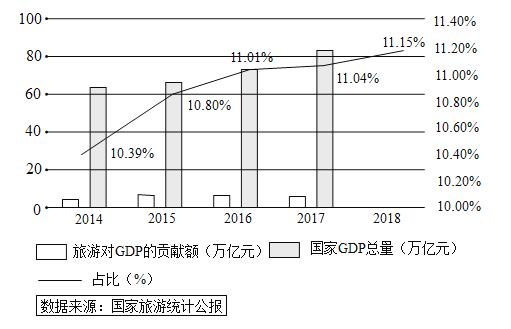
(1)根据以上数据,求出占比![]() 关于年份
关于年份![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)所求线性回归方程,预测2019年的旅游收入所占的比例.
附: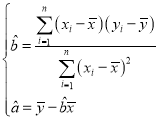 .
.