题目内容
20.若函数f(x)=$\frac{|sinx|}{x}$-k在(O,+∞)上恰有两个不同的零点x1、x2(x1<x2),给出下列4个结论:①tan(x1+$\frac{π}{4}$)=$\frac{1+{x}_{1}}{1-{x}_{1}}$;
②tan(x1+$\frac{π}{4}$)=$\frac{1-{x}_{1}}{1+{x}_{1}}$;
③tan(x2+$\frac{π}{4}$)=$\frac{1+{x}_{2}}{1-{x}_{2}}$;
④tan(x2+$\frac{π}{4}$)=$\frac{1-{x}_{2}}{1+{x}_{2}}$.
其中正确结论的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由f(x)=0,转化为|sinx|=kx,设g(x)=|sinx|,作出函数g(x)=|sinx|的图象,利用数学结合求出对应的切线方程,结合两角和差的正切公式进行求解即可.
解答  解:由f(x)=$\frac{|sinx|}{x}$-k=0,得|sinx|=kx,
解:由f(x)=$\frac{|sinx|}{x}$-k=0,得|sinx|=kx,
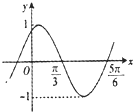
设g(x)=|sinx|,作出函数g(x)=|sinx|的图象如图,
如函数f(x)=$\frac{|sinx|}{x}$-k在(O,+∞)上恰有两个不同的零点,
则等价为函数g(x)=|sinx|与y=kx在(O,+∞)上恰有两个不同交点,
即y=kx与g(x)=|sinx|在(π,$\frac{3π}{2}$)上相切,
此时g(x)=|sinx|=-sinx,则切点坐标为(x2,-sinx2),
函数的导数g′(x)=-cosx,切线斜率为g′(x2)=-cosx2,
则切线方程为y-(-sinx2)=-cosx2(x-x2),
即y+sinx2=-cosx2(x-x2),
∵切线过原点,
∴sinx2=-cosx2(0-x2)=x2cosx2,
即tanx2=x2,
则tan(x2+$\frac{π}{4}$)=$\frac{tan{x}_{2}+tan\frac{π}{4}}{1-tan{x}_{2}tan\frac{π}{4}}$=$\frac{1+tan{x}_{2}}{1-tan{x}_{2}}$=$\frac{1+{x}_{2}}{1-{x}_{2}}$;
故C正确,
故正确的结论个数为1个,
故选:B.
点评 本题主要考查与函数有关的命题的真假判断,根据函数和方程之间的关系,转化为两个函数的交点问题,利用数形结合是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
8.函数f(x)=$\frac{{x}^{2}(x+1)}{x+1}$是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
10.已知全集U=R集合A={x|log2(x-1)},B={y|y=2x},则(CUA)∩B=( )
| A. | (-∞,0) | B. | (0,1] | C. | (-∞,1) | D. | (1,2) |
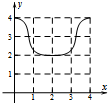
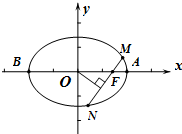 如图:已知方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的椭圆,A,B为顶点,过右焦点的弦MN的长度为y,中心O到弦MN的距离为d,点M从右顶点A开始按逆时针方向在椭圆上移动到B停止,当0°≤∠MFA≤90°时,记x=d,当90°<∠MFA≤180°,记x=2$\sqrt{2}$-d,函数y=f(x)图象是( )
如图:已知方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的椭圆,A,B为顶点,过右焦点的弦MN的长度为y,中心O到弦MN的距离为d,点M从右顶点A开始按逆时针方向在椭圆上移动到B停止,当0°≤∠MFA≤90°时,记x=d,当90°<∠MFA≤180°,记x=2$\sqrt{2}$-d,函数y=f(x)图象是( )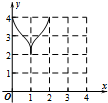
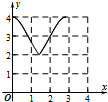
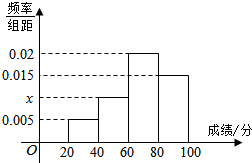 绵阳二诊后,某学校随机抽査部分学生的政治成绩进行统计分析,己知统计出的成绩频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100),己知低于60 分的人数是6人.
绵阳二诊后,某学校随机抽査部分学生的政治成绩进行统计分析,己知统计出的成绩频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100),己知低于60 分的人数是6人.