题目内容
已知数列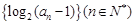 为等差数列,且
为等差数列,且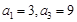 .
.
(1)求数列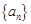 的通项公式;
的通项公式;
(2)证明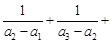 …
…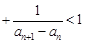 .
.
(1)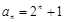 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)求数列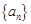 的通项公式,因为数列
的通项公式,因为数列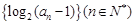 为等差数列,设公差为
为等差数列,设公差为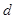 ,由
,由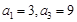 得
得 即
即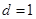 ,可写出数列
,可写出数列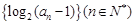 的通项公式,从而可得数列
的通项公式,从而可得数列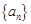 的通项公式;(2)证明
的通项公式;(2)证明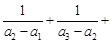 …
…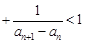 ,关键是求数列
,关键是求数列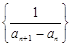 的通项公式,由(1)知
的通项公式,由(1)知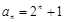 ,得
,得 ,这样数列
,这样数列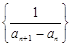 是一个以
是一个以 为首项,以
为首项,以 为公比的等比数列,由等比数列的前
为公比的等比数列,由等比数列的前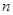 项和公式,求出和即可证出.
项和公式,求出和即可证出.
试题解析:(1)设等差数列的公差为d,
由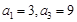 得
得 即d=1; 3分
即d=1; 3分
所以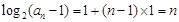 即
即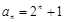 . 6分
. 6分
(2)证明: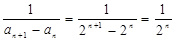 8分
8分
所以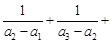
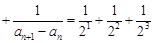
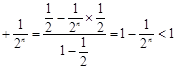 12分
12分
考点:等差数列的通项公式,等比数列求和.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
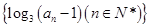 为等差数列,且
为等差数列,且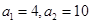 .
.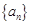 的通项公式;
的通项公式;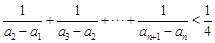 .
.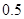 万人,从2023年开始到2032年每年人口为上一年的99%.
万人,从2023年开始到2032年每年人口为上一年的99%. 年的人口总数
年的人口总数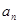 的表达式(注:2013年为第一年);
的表达式(注:2013年为第一年);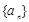 满足
满足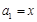 ,
,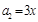 ,
,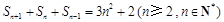 ,
,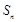 是数列
是数列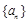 的前
的前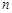 项和.
项和.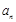 ;
;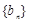 满足
满足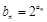 ,数列
,数列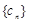 满足
满足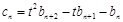 ,试比较数列
,试比较数列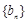 前
前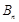 与
与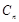 的大小;
的大小;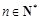 ,
,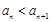 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.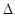 ABC中,三个内角A,B,C的对边分别为
ABC中,三个内角A,B,C的对边分别为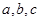 ,且A,B,C成等差数列,
,且A,B,C成等差数列,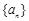 的前
的前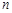 项和为
项和为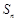 ,已知
,已知 ,
,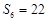 .
.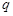 的等比数列
的等比数列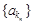 ,其中
,其中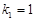 ,且
,且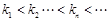 ,
,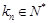 .
.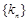 的通项公式;
的通项公式; 的不等式
的不等式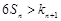 有解,试求
有解,试求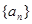 满足
满足 (
( ).
).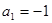 ,
, (
( 和
和 的值,使得数列
的值,使得数列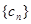 为等比数列;并求此时数列
为等比数列;并求此时数列 是等差数列
是等差数列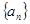 的前
的前 项和,满足
项和,满足 ;
;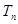 是数列
是数列 的前
的前 .
. 的前
的前 .
.