题目内容
(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(文)已知数列 中,
中,
(1)求证数列 不是等比数列,并求该数列的通项公式;
不是等比数列,并求该数列的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)设数列 的前
的前 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值.
(文)已知数列
 中,
中,
(1)求证数列
 不是等比数列,并求该数列的通项公式;
不是等比数列,并求该数列的通项公式;(2)求数列
 的前
的前 项和
项和 ;
;(3)设数列
 的前
的前 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值.(1)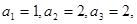
 ,
,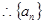 不是等比数列;………2分
不是等比数列;………2分
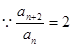 ,
,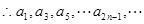 及
及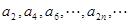 成等比数列,
成等比数列,
公比为2,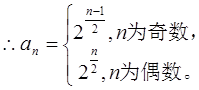 ……………6分
……………6分
(2)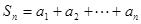 ,
,
当 为偶数时,
为偶数时,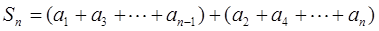
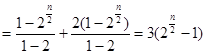 ;……………8分
;……………8分
当 为奇数时,
为奇数时,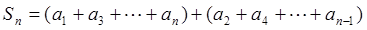
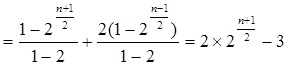 .……………10分
.……………10分
因此,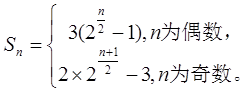 ……………12分
……………12分
(3)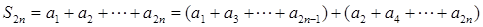
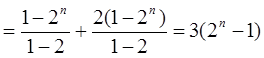 。 ……………13分
。 ……………13分
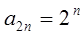 , ……………14分
, ……………14分
因此不等式为 3(1-k2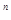 )
)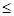 3(
3(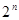 -1)2
-1)2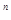 ,
,
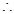 k
k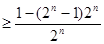 ,即k
,即k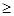
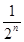 -(2
-(2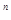 -1),
-1),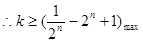
……………16分
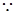 F(n)=
F(n)=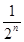 -(2
-(2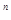 -1)单调递减;
-1)单调递减;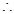 F(1)=
F(1)= 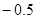 最大,
最大,
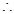

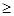
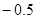 ,即
,即 的最小值为
的最小值为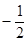 。……………18分
。……………18分
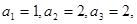
 ,
,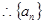 不是等比数列;………2分
不是等比数列;………2分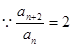 ,
,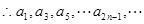 及
及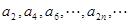 成等比数列,
成等比数列,公比为2,
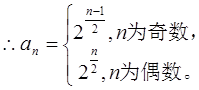 ……………6分
……………6分(2)
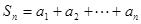 ,
,当
 为偶数时,
为偶数时,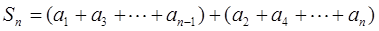
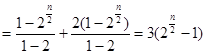 ;……………8分
;……………8分当
 为奇数时,
为奇数时,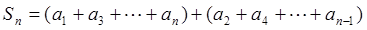
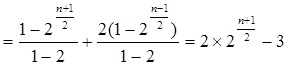 .……………10分
.……………10分因此,
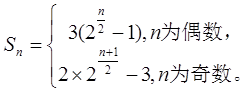 ……………12分
……………12分(3)
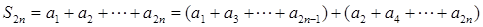
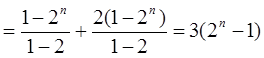 。 ……………13分
。 ……………13分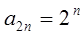 , ……………14分
, ……………14分因此不等式为 3(1-k2
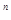 )
)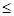 3(
3(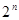 -1)2
-1)2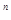 ,
,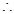 k
k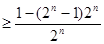 ,即k
,即k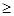
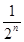 -(2
-(2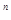 -1),
-1),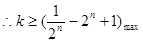
……………16分
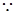 F(n)=
F(n)=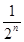 -(2
-(2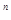 -1)单调递减;
-1)单调递减;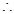 F(1)=
F(1)= 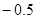 最大,
最大,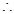

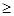
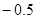 ,即
,即 的最小值为
的最小值为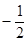 。……………18分
。……………18分略

练习册系列答案
相关题目
 满足
满足 ,则
,则 ( )
( )



 满足
满足 ,
, ,
, ,则
,则 的
的


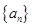 的前
的前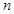 项和为
项和为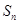 ,若对任意的
,若对任意的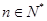 ,有
,有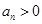 且
且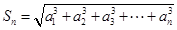 成立.
成立.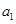 、
、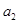 的值;
的值;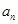 ;
;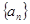 的前
的前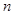 项和为
项和为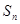 ,令
,令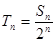 ,若对一切正整数
,若对一切正整数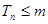 ,求
,求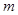 的取值范围.
的取值范围.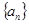 满足
满足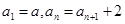 。定义数列
。定义数列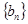 ,使得
,使得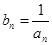 ,
,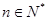 。若4<
。若4<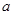 < 6,则数列
< 6,则数列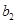
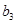
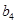
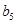
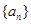 的各项均为正数,且
的各项均为正数,且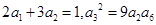 .
.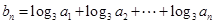 ,求数列
,求数列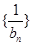 的前n项和.
的前n项和.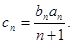 ,求数列{
,求数列{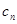 }的前
}的前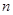 项和.
项和.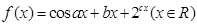 ,
,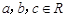 且为常数。若存在一公差大于
且为常数。若存在一公差大于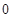 的等差数列
的等差数列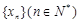 ,使得
,使得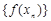 为一公比大于
为一公比大于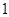 的等比数列,请写出满足条件的一组
的等比数列,请写出满足条件的一组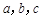 的值 .(答案不唯一,一组即可)
的值 .(答案不唯一,一组即可)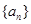 中,若
中,若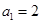 ,且对任意的正整数
,且对任意的正整数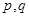 都有
都有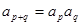 ,
,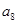 的值为 .
的值为 .