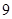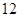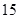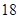题目内容
设等差数列 的公差
的公差 ,
, ,若
,若 是
是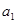 与
与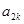 的等比中项,则
的等比中项,则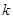 =( )
=( )
| A.3或6 | B.3 或9 | C.3 | D.6 |
B
解析试题分析:因为等差数列 的公差
的公差 ,又
,又 是
是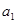 与
与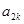 的等比中项,所以可得
的等比中项,所以可得 .又因为
.又因为 .所以
.所以 .化简得.
.化简得. 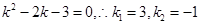 (舍去)故选B.
(舍去)故选B.
考点:1.等差数列.2等比数列.3.数列的通项公式.4.化简方程的能力

练习册系列答案
相关题目
等差数列 中,
中,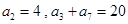 ,则
,则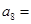 ( )
( )
| A.8 | B.12 | C.16 | D.24 |
《张丘建算经》卷上第22题——“女子织布”问题:某女子善于织布,一天比一天织得快,而且每天增加的数量相同.已知第一天织布5尺,30天共织布390尺,则该女子织布每天增加( )
A. 尺 尺 | B. 尺 尺 | C. 尺 尺 | D. 尺 尺 |
已知数列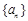 是等差数列,
是等差数列, ,设
,设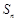 为数列
为数列 的前
的前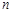 项和,则
项和,则 ( )
( )
| A.2014 | B.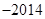 | C.3021 | D.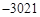 |
设等差数列 的前
的前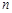 项和为
项和为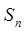 ,
,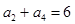 ,则
,则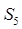 等于( )
等于( )
| A.10 | B.12 | C.15 | D.30 |
已知各项不为0的等差数列 满足
满足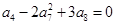 ,数列
,数列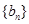 是等比数列,且
是等比数列,且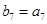 ,则
,则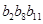 等于( )
等于( )
| A.1 | B.2 | C.4 | D.8 |
若数列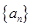 满足
满足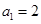 ,
,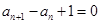
 ,则其通项
,则其通项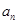 =( )
=( )
A.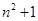 | B.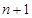 | C.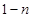 | D.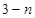 |
下面是关于公差d>0的等差数列{an}的四个命题:
p1:数列{an}是递增数列;p2:数列{nan}是递增数列;
p3:数列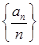 是递增数列;p4:数列{an+3nd}是递增数列.
是递增数列;p4:数列{an+3nd}是递增数列.
其中的真命题为( ).
| A.p1,p2 | B.p3,p4 |
| C.p2,p3 | D.p1,p4 |
 的三边长成公差为
的三边长成公差为 的等差数列,且最大角的正弦值为
的等差数列,且最大角的正弦值为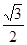 ,则这个三角形的周长是( )
,则这个三角形的周长是( )