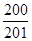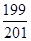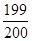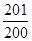题目内容
已知数列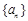 是等差数列,
是等差数列, ,设
,设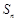 为数列
为数列 的前
的前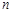 项和,则
项和,则 ( )
( )
| A.2014 | B.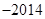 | C.3021 | D.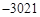 |
C
解析试卷分析: ,则公差
,则公差 ,所以
,所以
方法一:
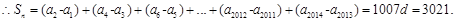
方法二:(错位相减)
由于 ,则
,则
①式两边分别乘以(-1),得②式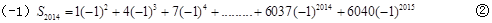
①-②得
 .
.
考点:1.等差数列的通项公式;2.错位相减法求前n项和的求法.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知等差数列:5, …的前n项和为Sn,则使得Sn取得最大值的n的值为( )
…的前n项和为Sn,则使得Sn取得最大值的n的值为( )
| A.7 | B.8 | C.7或8 | D.8或9 |
等差数列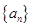 的前n项和为
的前n项和为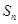 ,且
,且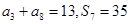 ,则
,则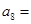 ( )
( )
| A.8 | B.9 | C.1 0 | D.11 |
设等差数列 的公差
的公差 ,
, ,若
,若 是
是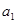 与
与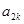 的等比中项,则
的等比中项,则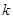 =( )
=( )
| A.3或6 | B.3 或9 | C.3 | D.6 |
等差数列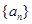 的前
的前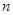 项和为
项和为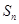 ,且
,且 ,则公差
,则公差 等于( )
等于( )
A.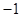 | B.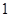 | C. | D. |
已知 为等差数列,且
为等差数列,且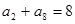 ,
,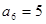 ,则Sl0的值为
,则Sl0的值为
| A.50 | B.45 | C.55 | D.40 |
已知等差数列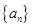 中,
中,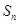 为其前n项和,若
为其前n项和,若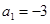 ,
,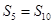 ,则当
,则当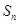 取到最小值时n的值为( )
取到最小值时n的值为( )
| A.5 | B.7 | C.8 | D.7或8 |
等差数列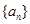 的前n项和为
的前n项和为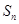 ,且满足
,且满足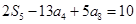 ,则下列数中恒为常数的是( )
,则下列数中恒为常数的是( )
A.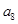 | B.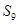 | C.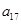 | D.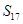 |
 的前200项和为 ( ).
的前200项和为 ( ).