题目内容
7.若方程|x2-2x-1|-t=0有四个不同的实数根x1、x2、x3、x4,且x1<x2<x3<x4,则2(x4-x1)+(x3-x2)的取值范围是( )| A. | (8,6$\sqrt{2}$) | B. | (6$\sqrt{2}$,4$\sqrt{5}$) | C. | [8,4$\sqrt{5}$] | D. | (8,4$\sqrt{5}$] |
分析 先作函数y=|x2-2x-1|的图象,结合图象可得0<t<2,再由韦达定理可得x4-x1=$\sqrt{{2}^{2}+4(1+t)}$=$\sqrt{8+4t}$,x3-x2=$\sqrt{8-4t}$,再令f(t)=2$\sqrt{8+4t}$+$\sqrt{8-4t}$,令f′(t)=$\frac{4\sqrt{8-4t}-2\sqrt{8+4t}}{\sqrt{8+4t}\sqrt{8-4t}}$=0得t=$\frac{6}{5}$,从而由函数的单调性确定2(x4-x1)+(x3-x2)的取值范围.
解答 解:由题意,
作函数y=|x2-2x-1|的图象如下,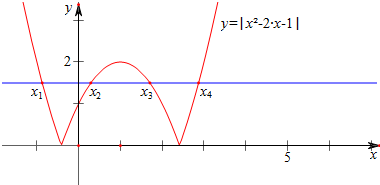
由图象知,0<t<2,
∵|x2-2x-1|-t=0,
∴|x2-2x-1|=t,
故x2-2x-1-t=0或x2-2x-1+t=0,
则x4-x1=$\sqrt{{2}^{2}+4(1+t)}$=$\sqrt{8+4t}$,
x3-x2=$\sqrt{8-4t}$,
故2(x4-x1)+(x3-x2)
=2$\sqrt{8+4t}$+$\sqrt{8-4t}$,
令f(t)=2$\sqrt{8+4t}$+$\sqrt{8-4t}$,
令f′(t)=$\frac{4\sqrt{8-4t}-2\sqrt{8+4t}}{\sqrt{8+4t}\sqrt{8-4t}}$=0得,
t=$\frac{6}{5}$,
故f(t)在(0,$\frac{6}{5}$)上是增函数,在($\frac{6}{5}$,2)上是减函数;
而f($\frac{6}{5}$)=4$\sqrt{5}$,f(0)=6$\sqrt{2}$,f(2)=8;
故2(x4-x1)+(x3-x2)的取值范围是(8,4$\sqrt{5}$],
故选:D.
点评 本题考查了导数的综合应用及数形结合的应用,属于中档题.

| A. | (1,2) | B. | (2,+∞) | C. | (1,$\root{3}{4}$) | D. | ($\root{3}{4}$,2) |
 四棱锥P-ABCD中,PA⊥底面ABCD,PA=2$\sqrt{3}$,BC=CD=2,∠ACB=∠ACD=$\frac{π}{3}$
四棱锥P-ABCD中,PA⊥底面ABCD,PA=2$\sqrt{3}$,BC=CD=2,∠ACB=∠ACD=$\frac{π}{3}$ 如图,已知四边形ABCD,EADM,MDCF都是边长为2的正方形,点P,Q分别是ED,AC的中点.
如图,已知四边形ABCD,EADM,MDCF都是边长为2的正方形,点P,Q分别是ED,AC的中点.