题目内容
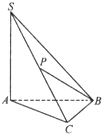 (2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )
(2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )分析:根据面面垂直的判定与性质,作AC的垂线可得异面直线所成的角,再通过解三角形求解即可.
解答: 解:过P作PO⊥AC,垂足为O,连接BO.
解:过P作PO⊥AC,垂足为O,连接BO.
∵SA⊥AC,∴PO∥SA,∴∠OPB为异面直线SA与PB所成的角.
∵SA丄平面ABC,∴平面SAC⊥平面ABC,
∴PO⊥平面ABC,BO?平面ABC,∴PO⊥BO.
∵点P是SC的中点,OP∥SA,∴PO=
=
,
在△ABC中,AC=2,AB丄BC,∵O是AC的中点,∴BO=1
在Rt△POB中,PB=
∴sin∠OPB=
.
∴异面直线SA与PB所成角的正弦值为
故选C
 解:过P作PO⊥AC,垂足为O,连接BO.
解:过P作PO⊥AC,垂足为O,连接BO.∵SA⊥AC,∴PO∥SA,∴∠OPB为异面直线SA与PB所成的角.
∵SA丄平面ABC,∴平面SAC⊥平面ABC,
∴PO⊥平面ABC,BO?平面ABC,∴PO⊥BO.
∵点P是SC的中点,OP∥SA,∴PO=
| SA |
| 2 |
| 3 |
| 2 |
在△ABC中,AC=2,AB丄BC,∵O是AC的中点,∴BO=1
在Rt△POB中,PB=
| ||
| 2 |
∴sin∠OPB=
2
| ||
| 13 |
∴异面直线SA与PB所成角的正弦值为
2
| ||
| 13 |
故选C
点评:本题考查异面直线所成的角.异面直线所成的角的求法是:1、作角(作平行线);2、证角(符合定义);3、求角(解三角形).

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 (2013•成都一模)如图,在△ABC中,
(2013•成都一模)如图,在△ABC中, (2013•成都一模)如图,矩形 ABCD 中,BC=2,AB=1,PA丄平面 ABCD,BE∥PA,BE=
(2013•成都一模)如图,矩形 ABCD 中,BC=2,AB=1,PA丄平面 ABCD,BE∥PA,BE=