题目内容
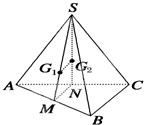 如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( )
如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( )分析:根据三角形的重心定理,可得SG1=
SM且SG2=
SN,因此△SMN中,由比例线段证出G1G2∥MN.在△ABC中利用中位线定理证出MN∥BC,可得直线G1G2与BC的位置关系是平行.
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:∵△SAB中,G1为的重心,
∴点G1在△SAB中线SM上,且满足SG1=
SM
同理可得:△SAC中,点G2在中线SN上,且满足SG2=
SN
∴△SMN中,
=
,可得G1G2∥MN
∵MN是△ABC的中位线,∴MN∥BC
因此可得G1G2∥BC,即直线G1G2与BC的位置关系是平行
故选:B
∴点G1在△SAB中线SM上,且满足SG1=
| 2 |
| 3 |
同理可得:△SAC中,点G2在中线SN上,且满足SG2=
| 2 |
| 3 |
∴△SMN中,
| SG1 |
| SM |
| SG2 |
| SN |
∵MN是△ABC的中位线,∴MN∥BC
因此可得G1G2∥BC,即直线G1G2与BC的位置关系是平行
故选:B
点评:本题给出三棱锥两个侧面的重心的连线,判定它与底面相对棱的位置关系,着重考查了三角形重心的性质、比例线段的性质和三角形中位线定理等知识,属于基础题.

练习册系列答案
相关题目
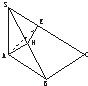 如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.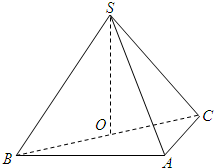 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2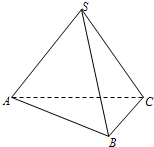 (2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( )
(2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( )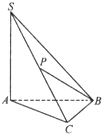 (2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )
(2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )