题目内容
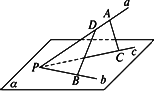
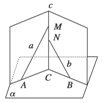
如图所示,已知直线a与b不共面,直线c∩a=M,直线b∩c=N,又a∩平面α=A,b∩平面α=B,c∩平面α=C,求证:A、B、C三点不共线.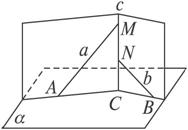
思路解析:此题属于否定形式的命题,所以应采用反证法.
证明:假设A、B、C三点共线于直线l,
∵A、B、C∈α,∴l
α.
∵c∩l=C,∴c与l可确定一个平面β.
∵c∩a=M,∴M∈β.又A∈l,
∴a
β.同理,b
β.∴直线a与b共面.
这与已知矛盾.∴A、B、C三点不共线.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，已知直线l：3x+4y-12=0与x，y轴的正半轴分别交于A，B两点，直线l1和AB，OA分别交于C，D，且平分△AOB的面积，求CD的最小值．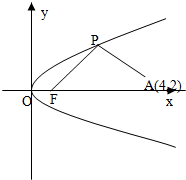
如图所示，已知直线l的斜率为k且过点Q（-3，0），抛物线C：y2=16x，直线与抛物线l有两个不同的交点，F是抛物线的焦点，点A（4，2）为抛物线内一定点，点P为抛物线上一动点．
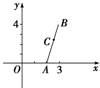如图所示，已知两点A（2，0），B（3，4），直线ax-2y=0与线段AB交于点C，且C分
