题目内容
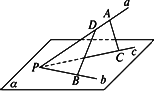
如图所示,已知直线a、b、c不共面,P是它们的公共点,A∈a,D∈a,B∈b,C∈c,A、B、C、D四点不与P重合,求证:BD和AC是异面直线.
答案:
解析:
解析:
思路解析:方法一:用反证法;
方法二:用异面直线的判定定理“过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线”.
证法一:假设BD和AC不是异面直线,则可设BD和AC共面于α,
∴A∈α,B∈α,C∈α,D∈α.
∵A∈α,D∈α,∴a![]() α.
α.
又P是a、b、c的公共点,∴P∈α.
∵B∈b,C∈c,c![]() α,
α,
∴a、b、c三线共面,这与已知a、b、c不共面矛盾.
∴假设不成立.故BD和AC是异面直线.
证法二:由已知,得D∈平面APC,AC![]() 平面APC,D
平面APC,D![]() AC,B
AC,B![]() 平面APC.根据异面直线的判定定理得BD和AC是异面直线.
平面APC.根据异面直线的判定定理得BD和AC是异面直线.

练习册系列答案
相关题目
 如图所示,已知直线l:3x+4y-12=0与x,y轴的正半轴分别交于A,B两点,直线l1和AB,OA分别交于C,D,且平分△AOB的面积,求CD的最小值.
如图所示,已知直线l:3x+4y-12=0与x,y轴的正半轴分别交于A,B两点,直线l1和AB,OA分别交于C,D,且平分△AOB的面积,求CD的最小值.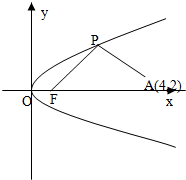 如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.
如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.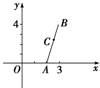 如图所示,已知两点A(2,0),B(3,4),直线ax-2y=0与线段AB交于点C,且C分
如图所示,已知两点A(2,0),B(3,4),直线ax-2y=0与线段AB交于点C,且C分