题目内容

精英家教网已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，其左右焦点分别为F1、F2，A、B分别为椭圆的上、下顶点，如果四边形AF1BF2为边长为2的正方形．
（Ⅰ）求椭圆C的方程；
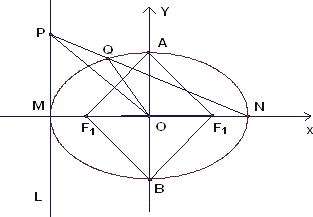
（Ⅱ）设椭圆的左、右顶点为M，N，过点M作x轴的垂线l，在l上任取一点P，连接PN交椭圆C于Q，探究
OP
•
OQ
是否为定值？如果是，求出定值；如果不是，请说明理由．
分析：（1）四边形AF1BF2是边长为2的正方形，求得a和b，则椭圆的方程可得．
（2）设直线PN：y=k（x-a），则P点坐标可知，把直线方程与椭圆方程联立消去y，根据韦达定理求得a•xQ的表达式，进而求得xQ的表达式，代入直线方程求得yQ的表达式，表示出
OP
•
OQ
，结果为定值．
解答：解：（Ⅰ）∵四边形AF1BF2是边长为2的正方形，
∴a=2，b=c=
2

∴椭圆的方程为
x2
4
+
y2
2
=1
（Ⅱ）设直线PN：y=k（x-a），
∴P（-a，-2ka）
∵
y=k(x-a)
x2+2y2=4
?(1+2k2)x2-4k2ax+2k2a2-4=0
∴a•xQ=
2k2a2-4
1+2k2
?xQ=
2k2a2-4
(1+2k2)a
yQ=k(
2k2a2-4
(1+2k2)a
-a)=
-(a2+4)k
a(1+2k2)

∴
OP
•
OQ
=xPxQ+yPyQ=
4-2k2a2
1+2k2
+
2k2(4+a2)
1+2k2
=4定值．
点评：本题主要考查了椭圆的标准方程，向量的基本计算，直线与椭圆的关系等．考查了学生综合分析问题的能力．
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
1
2
，且经过点P(1，
3
2
)．
（1）求椭圆C的方程；
（2）设F是椭圆C的左焦，判断以PF为直径的圆与以椭圆长轴为直径的圆的位置关系，并说明理由．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的短轴长为2
3
，右焦点F与抛物线y2=4x的焦点重合，O为坐标原点．
（1）求椭圆C的方程；
（2）设A、B是椭圆C上的不同两点，点D（-4，0），且满足
DA
=λ
DB
，若λ∈[
3
8
，
1
2
]，求直线AB的斜率的取值范围．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）经过点A（1，
3
2
），且离心率e=
3
2
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点B（-1，0）能否作出直线l，使l与椭圆C交于M、N两点，且以MN为直径的圆经过坐标原点O．若存在，求出直线l的方程；若不存在，说明理由．
（2012•房山区二模）已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的长轴长是4，离心率为
1
2
．
（Ⅰ）求椭圆方程；
（Ⅱ）设过点P（0，-2）的直线l交椭圆于M，N两点，且M，N不与椭圆的顶点重合，若以MN为直径的圆过椭圆C的右顶点A，求直线l的方程．
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的短轴长为2，离心率为
2
2
，设过右焦点的直线l与椭圆C交于不同的两点A，B，过A，B作直线x=2的垂线AP，BQ，垂足分别为P，Q．记λ=
AP+BQ
PQ
，若直线l的斜率k≥
3
，则λ的取值范围为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网