题目内容
 当x∈[-
当x∈[-| π |
| 6 |
| 2π |
| 3 |
| π |
| 2 |
(1)求函数f(x)在[-
| π |
| 6 |
| 2π |
| 3 |
(2)求方程f(x)=
| ||
| 2 |
| π |
| 6 |
| 2π |
| 3 |
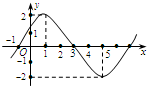
分析:(1)根据图象,
=
-
,可求得ω,利用ω•
+θ=
可求得θ,f(0)=
,可求得A;
(2)由
可求得其解集.
| T |
| 4 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| ||
| 2 |
(2)由
|
解答:解:(1)∵
=
-
=
,∴T=2π,ω=1;又1•
+θ=
,∴θ=
;由f(0)=
,得A=1;
∴f(x)=sin(x+
);
(2)由
解得:x=-
或x=
.
∴方程f(x)=
在[-
,
]的解集为:{-
,
}.
| T |
| 4 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| ||
| 2 |
∴f(x)=sin(x+
| π |
| 3 |
(2)由
|
| π |
| 12 |
| 5π |
| 12 |
∴方程f(x)=
| ||
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查其周期,相位,与振幅的确定,属于中档题.

练习册系列答案
相关题目
 已知函数
已知函数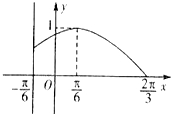 已知定义在区间[-π,
已知定义在区间[-π,