题目内容
 函数f(x)=Asin(ωx+φ),x∈R(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ),x∈R(A>0,ω>0,|φ|<| π |
| 2 |
| π |
| 2013 |
(1)求A、ω、φ的值;
(2)求m的最小值,并写出g(x)的表达式;
(3)若关于x的函数y=g(
| tx |
| 2 |
| π |
| 3 |
| π |
| 4 |
分析:(1)由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,从而求得A、ω、φ的值.
(2)由图易知,m的最小值为
,故g(x)=2sin2x.
(3)根据函数y=g(
)=2sintx 的周期为
,当t>0时,结合图象可得-
•
≥-
,由此求得t的范围.当t<0时,由x在区间[-
,
]上,结合图象可得
•
≤
,由此求得t的范围.再把以上求得的t的范围取并集,即得所求.
(2)由图易知,m的最小值为
| π |
| 12 |
(3)根据函数y=g(
| tx |
| 2 |
| 2π |
| t |
| 1 |
| 4 |
| 2π |
| t |
| π |
| 3 |
| π |
| 3 |
| π |
| 4 |
| 1 |
| 4 |
| 2π |
| -t |
| π |
| 4 |
解答:解:(1)由函数的图象可得A=2,T=
=
+
,解得ω=2.
再由五点法作图可得 2×(-
)+φ=0,解得 φ=
.
(2)将y=f(x)的图象向右平移m(m>0)个单位,可得到函数y=g(x)的图象,且图象关于原点对称,
由图易知,m的最小值为
,且g(x)=2sin2x.
(3)关于x的函数y=g(
)=2sintx (t≠0),当t>0时,由x在区间[-
,
]上,结合图象可得
函数y=g(
)=2sintx 的周期为
,且满足-
•
≥-
,即
≤
,故 t≥
.
当t<0时,由x在区间[-
,
]上,结合图象可得
函数y=g(
)=2sintx 的周期为
,且满足
•
≤
,即
≤π,t≤-2.
综上可得,t≤-2 或 t≥
.
| 2π |
| ω |
| 11π |
| 12 |
| π |
| 12 |
再由五点法作图可得 2×(-
| π |
| 12 |
| π |
| 6 |
(2)将y=f(x)的图象向右平移m(m>0)个单位,可得到函数y=g(x)的图象,且图象关于原点对称,
由图易知,m的最小值为
| π |
| 12 |
(3)关于x的函数y=g(
| tx |
| 2 |
| π |
| 3 |
| π |
| 4 |
函数y=g(
| tx |
| 2 |
| 2π |
| t |
| 1 |
| 4 |
| 2π |
| t |
| π |
| 3 |
| 2π |
| t |
| 4π |
| 3 |
| 3 |
| 2 |
当t<0时,由x在区间[-
| π |
| 3 |
| π |
| 4 |
函数y=g(
| tx |
| 2 |
| 2π |
| -t |
| 1 |
| 4 |
| 2π |
| -t |
| π |
| 4 |
| 2π |
| -t |
综上可得,t≤-2 或 t≥
| 3 |
| 2 |
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,属于中档题.

练习册系列答案
相关题目
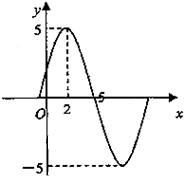 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R,|φ|<| π |
| 2 |
A、f(x)=5sin(
| ||||
B、f(x)=5sin(
| ||||
C、f(x)=5sin(
| ||||
D、f(x)=5sin(
|
 已知函数
已知函数 (2013•大连一模)已知函数
(2013•大连一模)已知函数 当
当