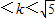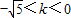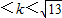题目内容
若过定点M(-1,0)且斜率为k的直线与圆x2+y2+4x-5=0在第一象限内的部分有交点,则k的取值范围是( )
A、0<k<
| ||
B、-
| ||
C、0<k<
| ||
| D、0<k<5 |
分析:把圆的方程化为标准形式,求出圆心和半径,由题意知,0<k<KMA,从而解出k的取值范围.
解答:解:圆的方程可变形为(x+2)2+y2=32,圆心(-2,0),半径等于3,令x=0,则y=±
.
设A(0,
),kMA=
.
又∵直线过第一象限且过(-1,0)点,∴k>0.又直线与圆在第一象限内有相交点,
∴k<
=
,∴0<k<
,故选 A.
| 5 |
设A(0,
| 5 |
| 5 |
又∵直线过第一象限且过(-1,0)点,∴k>0.又直线与圆在第一象限内有相交点,
∴k<
| ||
| 0+1 |
| 5 |
| 5 |
点评:本题考查直线和圆相交的性质,结合图形分析可得0<k<KMA,通过解此不等式可求得k的取值范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目