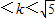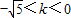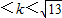Question

若过定点M（-1，0）且斜率为k的直线与圆x²+4x+y²-5=0在第一象限内的部分有交点，则k的取值范围是（　　）

• A．0＜k＜

  5

• B．-

  5

  ＜k＜0
• C．0＜k＜

  13

• D．0＜k＜5

Answer 1

分析：化简圆的方程求出圆与y正半轴的交点，画出图象，即可推出过定点M（-1，0）斜率为k的直线的范围．

解答：解：圆x²+4x+y²-5=0化为（x+2）²+y²=9，
圆与y正半轴交于（0，

5

），
因为过定点M（-1，0）且斜率为k的直线与圆x²+4x+y²-5=0在第一象限内的部分有交点，
如图，
所以k_MA＜k＜k_MB，
∴0＜k＜

5

1

，
∴0＜k＜

5

．
故选A．

点评：本题是中档题，考查数形结合的思想，直线斜率的求法，考查计算能力．