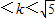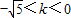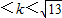Question

若过定点M（-1，0）且斜率为k的直线与圆x²+4x+y²-5=0在第一象限内的部分有交点，则k的取值范围是（　　）

• A、（0，

  5

  ）
• B、（-

  5

  ，0）
• C、（0，

  13

  ）
• D、（0，5）

Answer 1

分析：把圆的方程法化为标准形式，求出圆心和半径，并令圆方程中x=0，求出对应的y值，由题意知0＜k＜k_MA，从而解出k的取值范围．

解答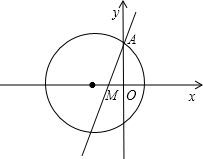：解：把圆的方程化为标准方程得：（x+2）²+y²=9，
∴圆心坐标为（-2，0），半径r=3，
令x=0，则y=±

5

，
设A（0，

5

），又M（-1，0），∴k_MA=

5

，
∵直线过第一象限且过（-1，0）点，∴k＞0，
又直线与圆在第一象限内有交点，
∴k＜

5 -0

0+1

=

5

，
∴k的取值范围是（0，

5

）．
故选A．

点评：点评：本题考查直线和圆的位置关系，考查了数形结合的思想，其中解题的关键是结合图形分析可得0＜k＜k_MA．