题目内容
19.已知A={x|x2+(2m-4)x+m2=0},A∩{x|x≤0}=∅,求m的取值范围.分析 由题意可得程x2+(2m-4)x+m2=0无实数根或有两个正实数根,然后分类转化为关于m的不等式(组)求解得答案.
解答 解:∵A={x|x2+(2m-4)x+m2=0},且A∩{x|x≤0}=∅,
方程x2+(2m-4)x+m2=0无实数根或有两个正实数根.
则(2m-4)2-4m2<0①,或$\left\{\begin{array}{l}{(2m-4)^{2}-4{m}^{2}≥0}\\{-2m+4>0}\\{{m}^{2}>0}\end{array}\right.$②,
解①得:m>1,
解②得:m≤1且m≠0.
∴m的取值范围是{m|m≠0}.
点评 本题考查交集及其运算,考查了分类讨论的数学思想方法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
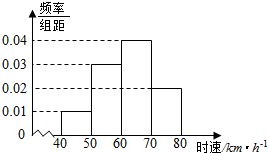 200辆汽车通过某一段公路时的时速频率分布直方图如图所示,则时速在(50,60)的汽车大约有60辆.
200辆汽车通过某一段公路时的时速频率分布直方图如图所示,则时速在(50,60)的汽车大约有60辆.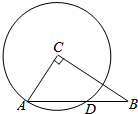 如图,已知在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,以C为圆心,CA为半径的圆交斜边于D,求AD.
如图,已知在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,以C为圆心,CA为半径的圆交斜边于D,求AD.