题目内容
设P(
,x)是角θ的终边上的点,且sinθ=
,则cosθ的值等于( )
| 2 |
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据sinθ=
,利用正弦的定义建立关于x的等式,解出x=1.从而得出r=|OP|=
,再利用余弦的定义即可算出cosθ的值.
| ||
| 3 |
| 3 |
解答:解:∵点P(
,x)是角θ的终边上的点,
∴r=|OP|=
,
又∵sinθ=
,
∴
=
,即
=
,
解得x2=1,得x=1(舍负)
因此r=
,可得cosθ=
=
=
.
故选:B
| 2 |
∴r=|OP|=
| 2+x2 |
又∵sinθ=
| ||
| 3 |
∴
| x |
| r |
| ||
| 3 |
| x | ||
|
| ||
| 3 |
解得x2=1,得x=1(舍负)
因此r=
| 3 |
| ||
| r |
| ||
|
| ||
| 3 |
故选:B
点评:本题给出角θ的终边上的点P的坐标,在已知sinθ的情况下求cosθ的值.着重考查了两点间的距离公式、任意角的三角函数的定义等知识,属于基础题.

练习册系列答案
相关题目
 选考题
选考题 如图是足球场的部分示意图,假设球门的宽AB=7m,A到边线的距离AC=30m.现距离边线5m处的一名运动员P沿着边线方向向底线运球,他观察球门的角∠APB称为视角.设P到底线的距离为PD=xm,tan∠APB记为y.
如图是足球场的部分示意图,假设球门的宽AB=7m,A到边线的距离AC=30m.现距离边线5m处的一名运动员P沿着边线方向向底线运球,他观察球门的角∠APB称为视角.设P到底线的距离为PD=xm,tan∠APB记为y.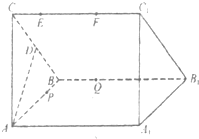 (2012•成都一模)设直三梭柱ABC-A1B1C1的底面为等腰直角三角形,AB=AC=2,动点E、F在侧棱CC1上,动点P、Q分别碰AB1,BB1上,若EF═1,CE=x,BQ=y,BP=z,其中x,y,z>0,则下列结论中错误的是.( )
(2012•成都一模)设直三梭柱ABC-A1B1C1的底面为等腰直角三角形,AB=AC=2,动点E、F在侧棱CC1上,动点P、Q分别碰AB1,BB1上,若EF═1,CE=x,BQ=y,BP=z,其中x,y,z>0,则下列结论中错误的是.( )