题目内容
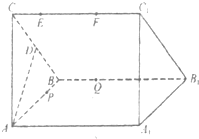 (2012•成都一模)设直三梭柱ABC-A1B1C1的底面为等腰直角三角形,AB=AC=2,动点E、F在侧棱CC1上,动点P、Q分别碰AB1,BB1上,若EF═1,CE=x,BQ=y,BP=z,其中x,y,z>0,则下列结论中错误的是.( )
(2012•成都一模)设直三梭柱ABC-A1B1C1的底面为等腰直角三角形,AB=AC=2,动点E、F在侧棱CC1上,动点P、Q分别碰AB1,BB1上,若EF═1,CE=x,BQ=y,BP=z,其中x,y,z>0,则下列结论中错误的是.( )分析:直三梭柱ABC-A1B1C1中,由EF∥平面AA1B1B,知EF∥平面 BPQ;当P与A重合、Q与B重合时,得到二面角P-EF-Q所成角的最大值;由EF∥BQ,知三棱锥P-EFQ的体积与z的变化有关,与x,y的变化无关;由AB=AC=2,D为线段BC的中点,知异面直线EQ和AD所成角为90°.
解答:解:∵直三梭柱ABC-A1B1C1中,EF∥平面AA1B1B,
∴EF∥平面 BPQ,故A正确;
∵直三梭柱ABC-A1B1C1的底面为等腰直角三角形,AB=AC=2,
∴当P与A重合、Q与B重合时,
二面角P-EF-Q所成角的最大值为∠ACB=
,故B正确;
∵EF∥BQ,∴S△EFQ为定值,
∴三棱锥P-EFQ的体积与z的变化有关,与x,y的变化无关,故C不正确;
∵AB=AC=2,D为线段BC的中点,
∴AD⊥平面BCC1B1,
∴异面直线EQ和AD所成角为90°,与x,y,z的变化无关,故D正确.
故选C.
∴EF∥平面 BPQ,故A正确;
∵直三梭柱ABC-A1B1C1的底面为等腰直角三角形,AB=AC=2,
∴当P与A重合、Q与B重合时,
二面角P-EF-Q所成角的最大值为∠ACB=
| π |
| 4 |
∵EF∥BQ,∴S△EFQ为定值,
∴三棱锥P-EFQ的体积与z的变化有关,与x,y的变化无关,故C不正确;
∵AB=AC=2,D为线段BC的中点,
∴AD⊥平面BCC1B1,
∴异面直线EQ和AD所成角为90°,与x,y,z的变化无关,故D正确.
故选C.
点评:本题考查直线与平面行的判断、二面角的求法、三棱锥体积的求法、异面直线所成角的大小的计算,解题时要认真审题,仔细解答

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目