题目内容
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为y=±$\sqrt{3}$x,左、右焦点分别为F1((-c,0),F2(c,0).且双曲线被直线x=-c所截得的弦长为6.(1)求双曲线C的方程;
(2)若过F2且倾斜角为135°的直线l交C于A,B两点,求△F1AB的面积.
分析 (1)由双曲线被直线x=-c所截得的弦长为6,得$\frac{{b}^{2}}{a}$=3,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为y=±$\sqrt{3}$x,得$\frac{b}{a}$=$\sqrt{3}$,求出a,b,即可求双曲线C的方程;
(2)设A(x1,y1),B(x2,y2),直线l方程:y=-(x-2).由双曲线方程与直线l方程消去y,得关于x的一元二次方程,利用根与系数的关系,即可求出△F1AB的面积.
解答 解:(1)x=-c时,y=±$\frac{{b}^{2}}{a}$,
∵双曲线被直线x=-c所截得的弦长为6,
∴$\frac{{b}^{2}}{a}$=3,
∵双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为y=±$\sqrt{3}$x,
∴$\frac{b}{a}$=$\sqrt{3}$,
∴a=1,b=$\sqrt{3}$,
∴双曲线C的方程为${x}^{2}-\frac{{y}^{2}}{3}$=1;
(2)设A(x1,y1),B(x2,y2),由右焦点F2(2,0),可得直线l方程:y=-(x-2)
代入双曲线方程,消去y,得2x2+4x-7=0
由根与系数的关系得:x1+x2=-2,x1x2=-$\frac{7}{2}$,y1-y2=-(x1-x2)
∴△F1AB的面积S=c|y1-y2|=2||x1-x2|=2$\sqrt{4+4×\frac{7}{2}}$=6$\sqrt{2}$.
点评 本题考查求双曲线的方程并探索焦点弦截得的三角形面积问题,着重考查了双曲线的标准方程、简单几何性质和直线与双曲线位置关系等知识点,属于中档题.

| A. | y轴对称 | B. | 直线y=-x对称 | C. | 坐标原点对称 | D. | 直线y=x对称 |
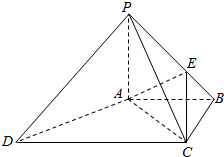 如图,四棱锥P-ABCD中,PA⊥底面ABCD,CD=2,底面ABCD为梯形,AB∥DC,AB⊥BC,AB=BC=PA=1,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,CD=2,底面ABCD为梯形,AB∥DC,AB⊥BC,AB=BC=PA=1,点E在棱PB上,且PE=2EB.