题目内容
运用旋转矩阵,求直线2x+y-1=0绕原点逆时针旋转45°后所得的直线方程.
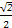 x+
x+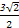 y-1=0
y-1=0旋转矩阵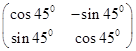 =
=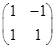 .
.
直线2x+y-1=0上任意一点(x0,y0)旋转变换后为(x'0,y'0),得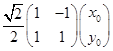 =
=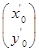 ,
,
∴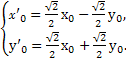
即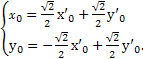
直线2x+y-1=0绕原点逆时针旋转45°后所得的直线方程是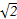 x+
x+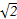 y-
y-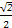 x+
x+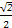 y-1=0,即
y-1=0,即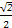 x+
x+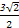 y-1=0.
y-1=0.
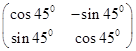 =
=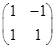 .
.直线2x+y-1=0上任意一点(x0,y0)旋转变换后为(x'0,y'0),得
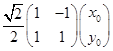 =
=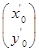 ,
,∴
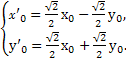
即
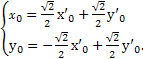
直线2x+y-1=0绕原点逆时针旋转45°后所得的直线方程是
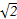 x+
x+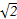 y-
y-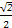 x+
x+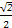 y-1=0,即
y-1=0,即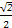 x+
x+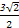 y-1=0.
y-1=0.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
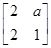 ,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P′(-4,0),求实数a的值;并求矩阵M的特征值及其对应的特征向量.
,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P′(-4,0),求实数a的值;并求矩阵M的特征值及其对应的特征向量.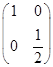 .
. ,3)在该变换作用下的象.
,3)在该变换作用下的象. =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.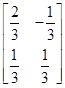 ,△ABC的顶点为A(0,0),B(2,0),C(1,2),求△ABC在矩阵M-1的变换作用下所得△A′B′C′的面积.
,△ABC的顶点为A(0,0),B(2,0),C(1,2),求△ABC在矩阵M-1的变换作用下所得△A′B′C′的面积. = .
= . 对应的变换是( )
对应的变换是( )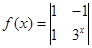 ,则
,则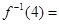 .
.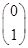 =
=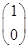 ,M
,M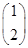 =
=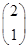 ,求M2.
,求M2.