题目内容
已知矩阵M=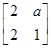 ,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P′(-4,0),求实数a的值;并求矩阵M的特征值及其对应的特征向量.
,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P′(-4,0),求实数a的值;并求矩阵M的特征值及其对应的特征向量.
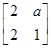 ,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P′(-4,0),求实数a的值;并求矩阵M的特征值及其对应的特征向量.
,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P′(-4,0),求实数a的值;并求矩阵M的特征值及其对应的特征向量.a=3.特征向量为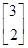 .特征值为-1与4.
.特征值为-1与4.
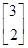 .特征值为-1与4.
.特征值为-1与4.由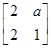
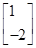 =
= ,∴2-2a=-4
,∴2-2a=-4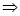 a=3.
a=3.
∴M= ,则矩阵M的特征多项式为
,则矩阵M的特征多项式为
f(λ)= =(λ-2)(λ-1)-6=λ2-3λ-4
=(λ-2)(λ-1)-6=λ2-3λ-4
令f(λ)=0,得矩阵M的特征值为-1与4.
当λ=-1时,
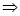 x+y=0,
x+y=0,
∴矩阵M的属于特征值-1的一个特征向量为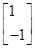 ;
;
当λ=4时,
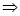 2x-3y=0,
2x-3y=0,
∴矩阵M的属于特征值4的一个特征向量为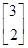 .
.
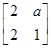
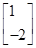 =
= ,∴2-2a=-4
,∴2-2a=-4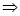 a=3.
a=3.∴M=
 ,则矩阵M的特征多项式为
,则矩阵M的特征多项式为f(λ)=
 =(λ-2)(λ-1)-6=λ2-3λ-4
=(λ-2)(λ-1)-6=λ2-3λ-4令f(λ)=0,得矩阵M的特征值为-1与4.
当λ=-1时,

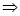 x+y=0,
x+y=0,∴矩阵M的属于特征值-1的一个特征向量为
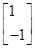 ;
;当λ=4时,

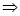 2x-3y=0,
2x-3y=0,∴矩阵M的属于特征值4的一个特征向量为
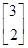 .
.
练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
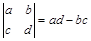 ,若
,若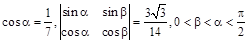 ,则
,则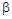 等于( )
等于( )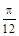
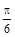
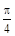
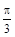
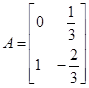 ,点
,点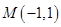 ,
, .求线段
.求线段 在矩阵
在矩阵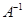 对应的变换作用下得到线段
对应的变换作用下得到线段 的长度.
的长度.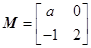 把直线
把直线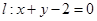 变换为另一条直线
变换为另一条直线 ,试求实数
,试求实数 值.
值.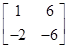 的特征值.
的特征值.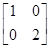 ,N=
,N=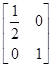 ,试求曲线y=sinx在矩阵MN变换下的曲线方程.
,试求曲线y=sinx在矩阵MN变换下的曲线方程.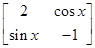 的值域.
的值域.