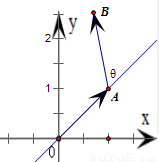
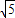题目内容
已知向量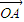 ,
,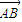 ,O是坐标原点,若|
,O是坐标原点,若|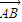 |=k|
|=k|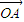 |,且
|,且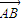 方向是沿
方向是沿 的方向绕着A点按逆时针方向旋转θ角得到的,则称
的方向绕着A点按逆时针方向旋转θ角得到的,则称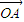 经过一次(θ,k)变换得到
经过一次(θ,k)变换得到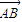 .现有向量
.现有向量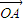 =(1,1)经过一次(θ1,k1)变换后得到
=(1,1)经过一次(θ1,k1)变换后得到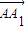 ,
,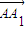 经过一次(θ2,k2)变换后得到
经过一次(θ2,k2)变换后得到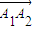 ,…,如此下去,
,…,如此下去,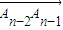 经过一次(θn,kn)变换后得到
经过一次(θn,kn)变换后得到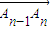 .设
.设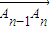 =(x,y),
=(x,y),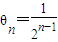 ,
,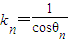 ,则y-x等于( )
,则y-x等于( )A.
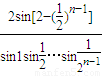
B.

C.
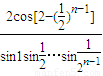
D.
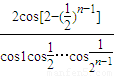
【答案】分析:根据题意,可得(θ1,k1)=(1,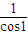 ),即当n=1时,一次(θ1,k1)变换将
),即当n=1时,一次(θ1,k1)变换将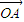 逆时针旋转1弧度,再将所得向量的长度再伸长为原来的
逆时针旋转1弧度,再将所得向量的长度再伸长为原来的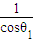 倍得到向量
倍得到向量 .因此当
.因此当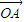 =(1,1)时,运用矩阵变换公式,算出
=(1,1)时,运用矩阵变换公式,算出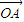 逆时针旋转1弧度所得向量
逆时针旋转1弧度所得向量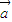 =(cos1-sin1,sin1+cos1),从而得到
=(cos1-sin1,sin1+cos1),从而得到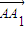 =(x,y)=(1-
=(x,y)=(1-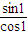 ,
,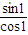 +1),所以y-x=
+1),所以y-x=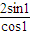 .接下来再对A、B、C、D各项在n=1时的情况进行计算,对照所得结果可得只有B项是正确的选项.
.接下来再对A、B、C、D各项在n=1时的情况进行计算,对照所得结果可得只有B项是正确的选项.
解答:解:根据题意,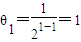 ,
,
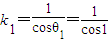
∴一次(θ1,k1)变换就是将向量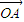 逆时针旋转1弧度,
逆时针旋转1弧度,
再将长度伸长为原来的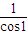 倍,
倍,
即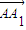 由
由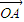 逆时针旋转1弧度而得,且
逆时针旋转1弧度而得,且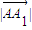 =
=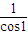
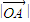
设向量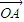 逆时针旋转1弧度,所得的向量为
逆时针旋转1弧度,所得的向量为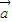 =(x',y')
=(x',y')
则有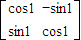 •
• =
= ,
,
∴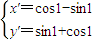 ,即向量
,即向量 逆时针旋转1弧度,
逆时针旋转1弧度,
得到向量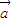 =(cos1-sin1,sin1+cos1),再将
=(cos1-sin1,sin1+cos1),再将 的模长度伸长为原来的
的模长度伸长为原来的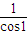 倍,
倍,
得到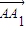 =
=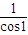 (cos1-sin1,sin1+cos1)=(1-
(cos1-sin1,sin1+cos1)=(1-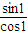 ,
,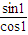 +1)
+1)
因此当n=1时,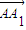 =(x,y)=(1-
=(x,y)=(1-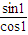 ,
,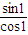 +1)
+1)
即 ,由此可得y-x=
,由此可得y-x=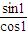 +1-(1-
+1-(1-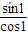 )=
)=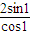
对于A,当n=1时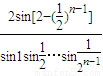 =
=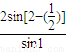 =
=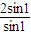 =2,与计算结果不相等,故A不正确;
=2,与计算结果不相等,故A不正确;
对于B,当n=1时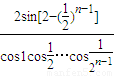 =
=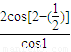 =
=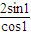 ,与计算结果相等,故B正确;
,与计算结果相等,故B正确;
对于C,当n=1时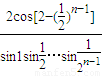 =
=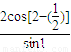 =
=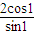 ,与计算结果不相等,故C不正确;
,与计算结果不相等,故C不正确;
对于D,当n=1时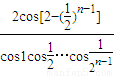 =
=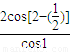 =
=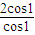 =2,与计算结果不相等,故D不正确
=2,与计算结果不相等,故D不正确
综上所述,可得只有B项符合题意
故选:B
点评:本题给出向量的旋转和伸缩,求向量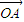 =(1,1)经过n变换(θn,kn)后得到的向量坐标,着重考查了向量的线性运算、用矩阵解决向量旋转问题和数列的通项公式等知识,属于中档题.
=(1,1)经过n变换(θn,kn)后得到的向量坐标,着重考查了向量的线性运算、用矩阵解决向量旋转问题和数列的通项公式等知识,属于中档题.
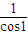 ),即当n=1时,一次(θ1,k1)变换将
),即当n=1时,一次(θ1,k1)变换将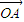 逆时针旋转1弧度,再将所得向量的长度再伸长为原来的
逆时针旋转1弧度,再将所得向量的长度再伸长为原来的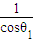 倍得到向量
倍得到向量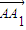 .因此当
.因此当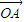 =(1,1)时,运用矩阵变换公式,算出
=(1,1)时,运用矩阵变换公式,算出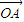 逆时针旋转1弧度所得向量
逆时针旋转1弧度所得向量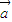 =(cos1-sin1,sin1+cos1),从而得到
=(cos1-sin1,sin1+cos1),从而得到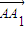 =(x,y)=(1-
=(x,y)=(1-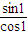 ,
,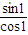 +1),所以y-x=
+1),所以y-x=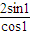 .接下来再对A、B、C、D各项在n=1时的情况进行计算,对照所得结果可得只有B项是正确的选项.
.接下来再对A、B、C、D各项在n=1时的情况进行计算,对照所得结果可得只有B项是正确的选项.解答:解:根据题意,
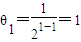 ,
,
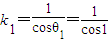
∴一次(θ1,k1)变换就是将向量
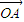 逆时针旋转1弧度,
逆时针旋转1弧度,再将长度伸长为原来的
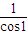 倍,
倍,即
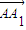 由
由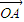 逆时针旋转1弧度而得,且
逆时针旋转1弧度而得,且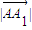 =
=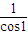
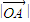
设向量
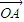 逆时针旋转1弧度,所得的向量为
逆时针旋转1弧度,所得的向量为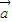 =(x',y')
=(x',y')则有
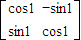 •
• =
= ,
,∴
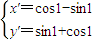 ,即向量
,即向量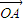 逆时针旋转1弧度,
逆时针旋转1弧度,得到向量
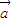 =(cos1-sin1,sin1+cos1),再将
=(cos1-sin1,sin1+cos1),再将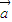 的模长度伸长为原来的
的模长度伸长为原来的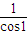 倍,
倍,得到
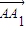 =
=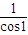 (cos1-sin1,sin1+cos1)=(1-
(cos1-sin1,sin1+cos1)=(1-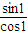 ,
,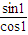 +1)
+1)因此当n=1时,
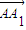 =(x,y)=(1-
=(x,y)=(1-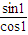 ,
,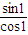 +1)
+1)即
 ,由此可得y-x=
,由此可得y-x=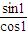 +1-(1-
+1-(1-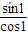 )=
)=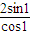
对于A,当n=1时
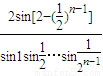 =
=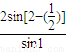 =
=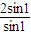 =2,与计算结果不相等,故A不正确;
=2,与计算结果不相等,故A不正确;对于B,当n=1时
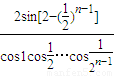 =
=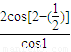 =
=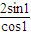 ,与计算结果相等,故B正确;
,与计算结果相等,故B正确;对于C,当n=1时
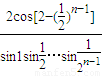 =
=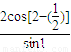 =
=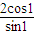 ,与计算结果不相等,故C不正确;
,与计算结果不相等,故C不正确;对于D,当n=1时
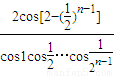 =
=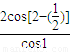 =
=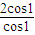 =2,与计算结果不相等,故D不正确
=2,与计算结果不相等,故D不正确综上所述,可得只有B项符合题意
故选:B
点评:本题给出向量的旋转和伸缩,求向量
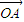 =(1,1)经过n变换(θn,kn)后得到的向量坐标,着重考查了向量的线性运算、用矩阵解决向量旋转问题和数列的通项公式等知识,属于中档题.
=(1,1)经过n变换(θn,kn)后得到的向量坐标,着重考查了向量的线性运算、用矩阵解决向量旋转问题和数列的通项公式等知识,属于中档题. 
练习册系列答案
相关题目
 ,其中O是坐标原点,若A,B,C三点共线,则实数k=( )
,其中O是坐标原点,若A,B,C三点共线,则实数k=( ) B.
B. C.11
D.
C.11
D.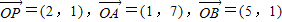 ,设M是直线OP上任意一点(O为坐标原点),则
,设M是直线OP上任意一点(O为坐标原点),则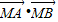 的最小值为( )
的最小值为( )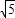
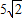
 ,设M是直线OP上任意一点(O为坐标原点),则
,设M是直线OP上任意一点(O为坐标原点),则 的最小值为( )
的最小值为( )