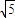题目内容
已知向量 ,设M是直线OP上任意一点(O为坐标原点),则
,设M是直线OP上任意一点(O为坐标原点),则 的最小值为( )
的最小值为( )A.-8
B.
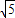
C.

D.8
【答案】分析:先设 ,然后表示
,然后表示 ,
, 求其数量积的表达式,再求其最小值.
求其数量积的表达式,再求其最小值.
解答:解:M是直线OP上任意一点(O为坐标原点),设 ,k∈R,则
,k∈R,则 =(1-2k,7-k),
=(1-2k,7-k), =(5-2k,1-k)
=(5-2k,1-k)
∴ =(1-2k)(5-2k)+(7-k)(1-k)=12-20k+5k2,当k=2时
=(1-2k)(5-2k)+(7-k)(1-k)=12-20k+5k2,当k=2时 的最小值是-8.
的最小值是-8.
故选A.
点评:本题考查平面向量的数量积,函数的最值等知识,是基础题.
 ,然后表示
,然后表示 ,
, 求其数量积的表达式,再求其最小值.
求其数量积的表达式,再求其最小值.解答:解:M是直线OP上任意一点(O为坐标原点),设
 ,k∈R,则
,k∈R,则 =(1-2k,7-k),
=(1-2k,7-k), =(5-2k,1-k)
=(5-2k,1-k)∴
 =(1-2k)(5-2k)+(7-k)(1-k)=12-20k+5k2,当k=2时
=(1-2k)(5-2k)+(7-k)(1-k)=12-20k+5k2,当k=2时 的最小值是-8.
的最小值是-8.故选A.
点评:本题考查平面向量的数量积,函数的最值等知识,是基础题.

练习册系列答案
相关题目
 ,设M是直线OP上任意一点(O为坐标原点),则
,设M是直线OP上任意一点(O为坐标原点),则 的最小值为( )
的最小值为( )

 ,设M是直线OP上任意一点(O为坐标原点),则
,设M是直线OP上任意一点(O为坐标原点),则 的最小值为( )
的最小值为( )
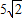
 ,设M是直线OP上任意一点(O为坐标原点),则
,设M是直线OP上任意一点(O为坐标原点),则 的最小值为( )
的最小值为( )

 ,设M是直线OP上任意一点(O为坐标原点),则
,设M是直线OP上任意一点(O为坐标原点),则 的最小值为( )
的最小值为( )