题目内容
20.一个圆锥与一个球的体积相等且圆锥的底面半径是球半径的2倍,若圆锥的高为1,则球的表面积为4π.分析 设出球的半径,求出球的体积,利用圆锥与球的体积相等,圆锥的高为1,求出球的半径,然后求出球的表面积.
解答 解:设球的半径为:r,则球的体积为:$\frac{4π}{3}{r}^{3}$.
∵圆锥与球的体积相等,圆锥的高为1,
∴$\frac{4π}{3}{r}^{3}$=$\frac{1}{3}π•(2r)^{2}•1$,
∴r=1,
∴球的表面积为:4πr2=4π.
故答案为:4π.
点评 本题考查圆锥与球的表面积与体积,考查计算能力,比较基础.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
11.已知变量x,y满足:$\left\{\begin{array}{l}{2x-y≤0}\\{x-2y+3≥0}\\{x≥0}\end{array}\right.$,则z=($\sqrt{2}$)2x+y的最大值为( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |

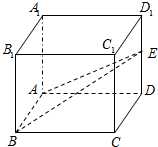 在正方体ABCD-A1B1C1D1中,E是棱DD1的中点,四棱锥E-ABCD的体积为$\frac{4}{3}$,求异面直线BE与B1A1所成的角的大小(结果用反三角函数值表示).
在正方体ABCD-A1B1C1D1中,E是棱DD1的中点,四棱锥E-ABCD的体积为$\frac{4}{3}$,求异面直线BE与B1A1所成的角的大小(结果用反三角函数值表示).