��Ŀ����
9��������˵�����ٺ���f��x��=$\frac{\sqrt{4-{x}^{2}}}{|x+3|-3}$Ϊ�溯����
����$\frac{cosx}{1-sinx}$=$\frac{1}{2}$����$\frac{cosx}{1+sinx}$=2��
�۶�����R�ϵĺ���f��x��=f��x+2������x��[3��5]ʱ��f��x��=2-|x-4|����f��cos3����f��sin3����
����֪����f��x��=$\left\{\begin{array}{l}{-{x}^{2}+2ax��x��1}\\{ax+1��x��1}\end{array}\right.$��������x1��x2��R����x1��x2��ʹ��f��x1��=f��x2������ʵ��a��ȡֵ��Χ�ǣ�-�ޣ�1���ȣ�2��+�ޣ���
������ȷ˵���Т٢ڢܣ�д��������ȷ˵������ţ�
���� ���ĸ�����ֱ�����жϣ��������溯���Ķ��壻������ͬ�����Ǻ����Ĺ�ϵ����ȷ����-1��x��1ʱ��x+4��[3��5]��f��x��=f��x+4��=2-|x|���ܷ������ۣ����ɵó����ۣ�
��� �⣺�ٺ����Ķ�����Ϊ{x|-2��x��2��x��0}��f��x��=$\frac{\sqrt{{4-x}^{2}}}{x}$Ϊ�溯������ȷ��
����$\frac{cosx}{1-sinx}$=$\frac{1}{2}$����$\frac{cosx}{1+sinx}$=2����ȷ��
�ۡ�f��x+2��=f��x����
�ຯ��f��x��������Ϊ2�����ں������ֵ�x��[3��5]ʱ��f��x��=2-|x-4|��
�൱-1��x��1ʱ��x+4��[3��5]����f��x��=f��x+4��=2-|x|����f��sin3��=2-sin3��2-��-cos3��=f��cos3��������
��������x1��x2��R����x1��x2��ʹ��f��x1��=f��x2����������˵��f��x����R�ϲ�������
�ٵ�a=0ʱ��f��x��=$\left\{\begin{array}{l}{-{x}^{2}��x��1}\\{1��x��1}\end{array}\right.$��������
��ͼ����ͼ��ʾ����������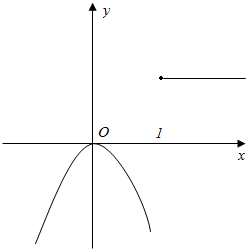
�ڵ�a��0ʱ������y=-x2+2ax�ĶԳ���x=a��0����ͼ����ͼ��ʾ����������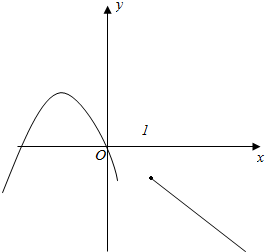
�۵�a��0ʱ������y=-x2+ax�ĶԳ���x=a��0����ͼ����ͼ��ʾ��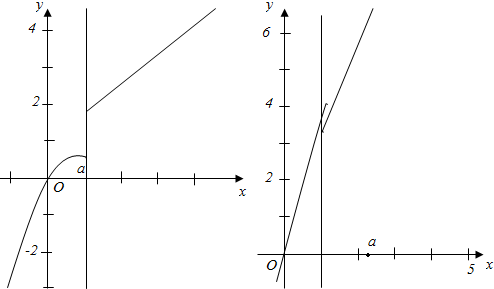
Ҫʹ��f��x����R�ϲ�����
��ֻҪ���κ����ĶԳ���x=a��1����$\left\{\begin{array}{l}{a��1}\\{-1+2a��a+1}\end{array}\right.$��
��0��a��1��a��2��
�ۺϵã�a��ȡֵ��Χ�ǣ�-�ޣ�1���ȣ�2��+�ޣ�������ȷ��
�ʴ�Ϊ���٢ڢܣ�
���� ���⿼�����������жϣ�����ѧ��������������������֪ʶ�ۺ���ǿ��

 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д� Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�| A�� | ��-�ޣ�-6�� | B�� | ��-�ޣ�-6] | C�� | ��-6��+�ޣ� | D�� | [-6��+�ޣ� |
| A�� | ��-�ޣ�$\frac{3}{2}$] | B�� | ��-�ޣ�1] | C�� | ��0��$\frac{9}{2}$�� | D�� | ��$\frac{1}{2}$��$\frac{9}{2}$] |
 ��ͼ��ʾ���Ǧ����ձ���ͼ����Ӱ���֣���ָ���Ǧ� �ķ�Χ��
��ͼ��ʾ���Ǧ����ձ���ͼ����Ӱ���֣���ָ���Ǧ� �ķ�Χ�� �У���
�У��� ��ֱ��
��ֱ�� ,��Բ
,��Բ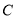 �İ뾶Ϊ
�İ뾶Ϊ ��Բ����
��Բ���� �ϣ�
�ϣ�
 Ҳ��ֱ��
Ҳ��ֱ��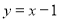 �ϣ�����
�ϣ����� ��Բ
��Բ �����ߣ������ߵķ��̣�
�����ߣ������ߵķ��̣�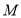 ��ʹ
��ʹ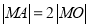 ����Բ��
����Բ�� ��ȡֵ��Χ��
��ȡֵ��Χ��